Simple Reverse-Time SDE Derivation for Diffusion Models

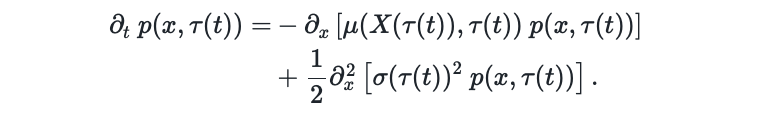
\(\newcommand{\Efunc}[1]{\mathbb{E}\left[ #1\right]} \newcommand{\Vfunc}[1]{\mathbb{V}\left[ #1\right]} \newcommand{\KL}[2]{\text{KL}\left[ #1 \ || \ #2 \right]} \newcommand{\denom}[1]{\frac{1}{#1}} \newcommand{\drift}{\mu(X_t, t)} \newcommand{\diff}{\sigma(X_t, t)}\)

We start out with the Fokker-Planck equation (FPE) which relates the change over time for the probability for a specific value of $x$ with a diffusion term $\sigma(t)$ which is only dependent on the time, \(\begin{align} \partial_t \ p(x,t) = & - \partial_x \left[ \drift \ p(x, t) \right] + \partial_x^2 \left[ \denom{2} \sigma(t)^2 \ p(x, t) \right] \\ = & - \partial_x \left[ \drift \ p(x, t) \right] + \denom{2} \sigma(t)^2 \partial_x^2 \left[ \ p(x, t) \right]. \end{align}\)

The FPE describes the evolution of the entire probability distribution of a stochastic process. We can simulate a single particle by defining the stochastic differential equation (SDE), \(\begin{align} dX_t = \underbrace{\mu(X_t, t) dt}_{\text{drift}} + \underbrace{\sigma(t) dW_t}_{\text{diffusion}} \end{align}\)

The importance of the FPE is its holistic approach of modelling the change of a basically infinite large ensemble of particles governed by the SDE above. Thus whereas simulating a single particle is nice and good, solving the FPE gives us the distribution of trajectories in a single go.

Imagine it as emptying a bucket of marbles onto a staircase which then bounce chaotically down the staircase. The SDE gives you the behavior of a single marble. The drift tells it to go down the staircase but the myriad of interactions and uneven parts of the staircase make it move seemingly random down the staircase. The individual trajectory of a marble is the SDE whereas the FPE tells us in an aggregate fashion where the marbles will be with what probability on the staircase. (Imagine using a million very tiny marbles to simulate the continuous limit.) At $t=0$ the probability of all marbles will be concentrated in your bucket. At $t=0.1$ they will spill out of the bucket and the probability will still be concentrated. But as soon as the marbles hit the first step they will start to disperse. In aggregate the marbles move down the staircase and thus the probability of a marble being at a specific point on the staircase will move also down. But some marbles will move slower and some marbles will move faster and thus the probability distribution of having a marble at a specific time at a specific point on the staircase will dissipate. After sufficient time they will all be at the bottom of the staircase in another bucket (we built a collection contraption). There the probability distribution will be highly concentrated again as all marbles will be found inside the very compact space of the bottom bucket.

So obtaining the FPE is of the harder, but more rewarding task as it gives us the underlying probability distribution over time and space instead of a bunch of trajectories.

Now we consider a time reversion $\color{blue}{\tau(t)} = 1 - t$ and are interested in what the change of the probability distribution is under this reversed time index, \(\begin{align} \partial_{t} \ p(x,\color{blue}{\tau(t)}) = & - \partial_x \left[ \mu(X(\color{blue}{\tau(t)}), \color{blue}{\tau(t)}) \ p(x, \color{blue}{\tau(t)}) \right] \\ & + \denom{2} \partial_x^2 \left[ \sigma(\color{blue}{\tau(t)})^2 \ p(x, \color{blue}{\tau(t)}) \right]. \end{align}\) With the time transformation $\color{blue}{\tau(t)}$, we apply the chain rule on the time transformation on the left hand side to obtain \(\begin{align} \frac{\partial p(x,\color{blue}{\tau(t)})}{\partial t} = \frac{ \partial p(x,\color{blue}{\tau(t)})}{\partial \tau} \ \frac{\partial \color{blue}{\tau(t)}}{\partial t} = \frac{ \partial p(x,\color{blue}{\tau(t)})}{\partial \tau} \ \underbrace{ \frac{\partial \color{blue}{\tau(t)}}{\partial t}}_{-1} = -\frac{ \partial p(x,\color{blue}{\tau(t)})}{\partial \tau}. \end{align}\) Then, we pull the negative factor from the chain rule to the right hand side and combine the drift and diffusion term into a single derivative via the distributive property of the partial derivative, \(\begin{align} \frac{ \partial p(x,\tau(t))}{\partial \tau} = & \partial_x \left[ \mu(X(\tau(t)), \tau(t)) \ p(x, \tau(t)) \right] - \denom{2} \sigma(\tau(t))^2 \color{blue}{\partial_x^2} \left[ \ p(x, \tau(t)) \right] \label{eq:app_reversetime_derivation1} \\ = & - \color{blue}{\partial_x} \Bigg[ -\mu(X(\tau(t)), \tau(t)) \ p(x, \tau(t)) + \denom{2} \sigma(\tau(t))^2 \color{blue}{\partial_x} \left[ \ p(x, \tau(t)) \right] \Bigg] \end{align}\) Applying the log derivative identity $\partial_x \log p(x) = \frac{1}{p(x)} \partial_x p(x)$, which rearranged yields $ \partial_x p(x) = p(x) \partial_x \log p(x)$, we obtain \(\begin{align} \frac{ \partial p(x,\tau(t))}{\partial \tau} = & - \partial_x \Bigg[ -\mu(X(\tau(t)), \tau(t)) \ p(x, \tau(t)) + \denom{2} \sigma(\tau(t))^2 \color{blue}{\partial_x \left[ \ p(x, \tau(t)) \right]} \Bigg] \\ & - \partial_x \Bigg[ -\mu(X(\tau(t)), \tau(t)) \ p(x, \tau(t)) + \denom{2} \sigma(\tau(t))^2 \color{blue}{\partial_x \log p(x, \tau(t)) p(x, \tau(t)} ) \Bigg] \\ = & - \partial_x \Bigg[ \Big( \underbrace{-\mu(X(\tau(t)), \tau(t)) + \denom{2} \sigma(\tau(t))^2 \color{blue}{\partial_x \log p(x, \tau(t))}}_{\text{reverse drift}} \Big) p(x, \tau(t))\Bigg]. \end{align}\)

The equation above states that the inverted drift with an additional scaled score term of the forward distribution will invert the stochastic process. If we read off the corresponding SDE we get \(\begin{align} dX(\tau) = \left\{-\mu(X(\tau(t)), \tau(t)) + \denom{2} \sigma(\tau(t))^2 \partial_x \log p(x, \tau(t)) \right\} dt \end{align}\)

Interestingly, there is no diffusion term occuring in this formulation of the reverse FPE (loud, surprised gasp! How shocking, dear!). We can in fact derive a more flexible reverse drift by returning to a slightly rearranged equation \ref{eq:app_reversetime_derivation1} with an additional, ‘neutral’ (because \(\pm\)) scaling factor $\alpha^2$. In the equations below, we incorporate the negative and the positive side of the additional diffusion in separate ways: \(\begin{align} \frac{ \partial p(x,\tau(t))}{\partial \tau} = & - \partial_x \left[ - \mu(X(\tau(t)), \tau(t)) \ p(x, \tau(t)) \right] - \denom{2} \sigma(\tau(t))^2 \partial_x^2 \left[ \ p(x, \tau(t)) \right] \nonumber \\ & \underbrace{\pm \ \frac{\alpha^2}{2} \ \sigma(\tau(t))^2 \partial_x^2 \left[ \ p(x, \tau(t)) \right]}_{\text{additional diffusion}} \\ = & - \partial_x \left[ - \mu(X(\tau(t)), \tau(t)) \ p(x, \tau(t)) \right] - \denom{2} \sigma(\tau(t))^2 \left( 1 + \alpha^2 \right) \partial_x^2 \left[ \ p(x, \tau(t)) \right] \\ & \underbrace{ + \ \frac{\alpha^2}{2} \ \sigma(\tau(t))^2 \partial_x^2 \left[ \ p(x, \tau(t)) \right]}_{\text{additional diffusion}} \\ = & - \partial_x \Bigg[ \Big( - \mu(X(\tau(t)), \tau(t)) + \denom{2} \sigma(\tau(t))^2 \left( 1 + \alpha^2 \right) \partial_x \log p(x, \tau(t)) \Big) \ p(x, \tau(t)) \Bigg] \nonumber \\ & + \ \partial_x^2 \left[ \frac{\alpha^2}{2} \ \sigma(\tau(t))^2 \ p(x, \tau(t)) \right]. \end{align}\)

from which we can infer the reverse drift consisting of the inverted original drift with the additionally scaled score with $\alpha$ and the additional diffusion, \(\begin{align} dX(\tau) = & \left\{ \overbrace{- \mu(X(\tau(t), \tau(t))}^{\text{reversed drift}} + \overbrace{\denom{2} \sigma(\tau(t))^2 \left( 1 + \alpha^2 \right) \partial_x \log p(x, \tau(t)) \Big)}^{\text{"diffusion correction"}} \right\} d\tau \\ & + \alpha \ \sigma(\tau(t)) dW(\tau) \end{align}\)

In the intuition is quite clear: If we add extra diffusion to our forward process, we will ‘diffuse’ more and the probability mass will be distributed over a larger, more spread out area. Therefore, if we want to invert this particular stochastic process, we need to increase the score term dependent on the \(\alpha\) which pushes the particles back into the high probability region.