Fokker, Planck & Kolmogorov Revisited

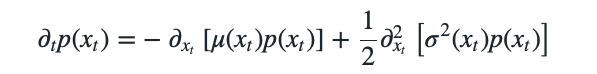
A Dutch, a German and a Russian walk into a bar …

At the core of the partial differential equations that will describe the change of a distribution both forward and backward in time lies the Chapman-Kolmogorov equation \(\begin{align} p(x_{t + \tau}) & = \int p(x_{t + \tau} , x'_{t}) \ dx'_t \\ & = \int p(x_{t + \tau} | x'_{t}) \ p(x'_t) \ dx'_t \end{align}\) which simply expands over an auxiliary variable $x’_t$ while simultaneously marginalizing it out and factorizing the joint distribution \(p(x_{t+\tau}, x'_t)\) into a conditional distribution. The conditional distribution above states that we can start from any \(x'_t\) and by moving to \(x_{t+\tau}\) with the right transition probability \(p(x_{t + \tau} | x'_{t})\) we will obtain the correct marginal distribution \(p(x_{t+\tau})\).

We will assume a stochastic differential equation the first two orders of which can be estimated with \(\begin{align} M^{(n)} (x'_t) = \int (x_{t+\tau} - x'_t)^n p(x_{t + \tau} | x'_t) dx_{t+\tau} \end{align}\) such that the dynamics are described by the Ito drift-diffusion process \(\begin{align} dX'_t = & M^{(1)}(X'_t) dt + M^{(2)}(X'_t) dW_t \\ = & \mu(X'_t, t) dt + \sigma(X'_t, t) dW_t \\ \end{align}\) with the Wiener process \(W_t\). The important part is to note the ‘direction’ of the differential which is evaluated strictly forward in time. We take \(x'_t\) as a sort of origin point which doesn’t change and weight the differential \(x_{t+\tau} - x'_t\) by the appropriate transition probability \(p(x_{t+\tau} | x'_t)\) over every possible \(x_{t+\tau}\).

Forward Equation

The Chapman-Kolmogorov equation fro the forward Kramers-Moyal expansion can be rewritten with the help of an auxilliary variable as \(\begin{align} p(x_{t + \tau}) = & \int p(x_{t + \tau} | x'_{t}) \ p(x'_t) \ dx'_t \\ = & \int_{X'} \int_{Y} \delta(y_{t+\tau} - x_{t+\tau}) p(y_{t + \tau} | x'_{t}) \ dy_{t+\tau} p(x'_t) dx'_t \end{align}\)

The main component of the Kramers-Moyal expansions is the use of the Taylor expansion on a shifted function. The classical Taylor expansion $T_{f,a}(x)$ of a function $f(x)$ around a root point $a$ says that we can reconstruct the function $f(x)$ with an infinite sum consisting of its derivatives \(\begin{align} T_{f,a}(x) = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!} (x - a)^n \end{align}\)

What happens if we introduce an offset $h$ to the root point $a$ which can take on any value we want? It turns out that the arbitrary offset $h$ can directly be used as a distance measure to the root point. The Taylor expansion of the shifted function $f(a + h)$ then becomes \(\begin{align} T_{f,a}(h) = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!} h^n \end{align}\)

We can then first expand the delta function $\delta ( y_{t+\tau} - x_{t+\tau} )$ with $\pm x_t$ and subsequently expand the Taylor series to obtain \(\begin{align} \delta(y_{t+\tau} - x_{t+\tau}) = & \delta(\overbrace{y_{t+\tau} - x'_t}^{h} + \overbrace{x'_t - x_{t+\tau}}^{a} ) \\ = & \sum_{n=0}^\infty \frac{1}{n!} \underbrace{\partial_{x'}^{n} \delta(x'_t - x_{t+\tau}) }_{f^{(n)}(a)} \underbrace{( y_{t+\tau} - x'_t)^n}_{h^n} \end{align}\)

We can plug the expanded Taylor series back in to get \(\begin{align} p(x_{t + \tau}) = & \int_{X'} \int_{Y} \overbrace{\delta(y_{t+\tau} - x_{t+\tau})}^{\text{Taylor Expansion}} p(y_{t + \tau} | x'_{t}) \ dy_{t+\tau} \ p(x'_t) dx'_t \\ = & \int_{X'} \int_{Y} \sum_{n=0}^\infty \frac{1}{n!} ( y_{t+\tau} - x'_t)^n \ \partial_{x'}^{n} \left[ \delta(x'_t - x_{t+\tau}) \right] p(y_{t + \tau} | x'_{t}) \ dy_{t+\tau} \ p(x'_t) dx'_t \\ = & \sum_{n=0}^\infty \frac{1}{n!} \int_{X'} \int_{Y} ( y_{t+\tau} - x'_t)^n \ \underbrace{ \partial_{x'}^{n} \left[ \delta(x'_t - x_{t+\tau})\right]}_{?} p(y_{t + \tau} | x'_{t}) \ dy_{t+\tau} \ p(x'_t) dx'_t \\ \end{align}\)

Now we need to find out, how to deal with the $n$’th derivative of Dirac delta function inside an integral.

A Quick Intermezzo on Delta Functions and Integration by Parts

In my work so far, I got the feeling that two mathematical tricks provide the most joy to physicists when they don’t know how to proceed: 1) Taylor Expansions and 2) Integration by Parts. We already encountered the Taylor expansion, so get ready to observe the second trick, integration by parts (IbP).

It should be first stated that the delta is a weird beast which is more or less only defined where it’s argument is zero. For $\delta(0)=1$ and $\delta(x)=0, x \neq 0$. For an integral of the product of $\int \delta(x=x’) f(x) dx = f(x’)$, the Dirac delta function serves as a sort of ‘selector’ which ignores any contribution of the integral except where $x=x’$ because only when $x=x’$ will it be one, otherwise zero.

Fortunately, we can yield the physicists favourite magic spell when dealing with probabilities: Integration by Parts. \(\begin{align} \int_{x=-\infty}^\infty u'(x) v(x) dx = \left[ u(x) v(x) \right]_{x=-\infty}^\infty - \int_{x=-\infty}^\infty u(x) v'(x) dx \end{align}\) which is the just integrating a rearranged product rule $(u(x) v(x))’ = u’(x) v(x) + u(x) v’(x)$ over the domain of $x$: \(\begin{align} \int_a^b (u(x) v(x))' dx &= \int_a^b u'(x) v(x) dx + \int_a^b u(x) v'(x) dx \\ & \Updownarrow \\ \int u'(x) v(x) dx &= \left[ u(x) v(x) \right]_{x=a}^b - \int_a^b u(x) v'(x) dx \end{align}\) where the integration cancels only the derivative of the product as the others are a product of a derivative and another function.

If the function $f(x)$ has compact support, meaning that ${f(x)=0 | x = \pm \infty }$, the the evaluation of the derivative-free component in integration by parts vanishes. So if we’re dealing with a probability distribution which is assumed to be zero at the far ends, we obtain the simplified term \(\begin{align} \int_{x=-\infty}^\infty \delta'(x) f(x) dx = \underbrace{\left[ \delta(x) f(x) \right]_{x=-\infty}^\infty}_{=0} - \int_{x=-\infty}^\infty \delta(x) f'(x) dx \end{align}\) For higher order derivatives this generalizes to \(\begin{align} \int_{x=-\infty}^\infty \delta^{(n)} (x) f(x) dx = \sum_k^{n-1} \left[ (-1)^k \delta^{(k)}(x) f^{(n-k)}(x) \right]_{x=-\infty}^\infty + (-1)^n \int_{x=-\infty}^\infty \delta(x) f^{(n)}(x) dx \end{align}\) which more or less moves the all the derivatives from the Dirac delta function over to $f(x)$ which is often called the ‘test function’ when inside an integral over the full domain. Since all the derivates and the function $f$ itself are zero at $x=\pm \infty$, $f^{(n)}(\pm \infty) = f(\pm \infty)=0 \ \forall n \in \mathbb{N}$, the term simplifies to \(\begin{align} \int_{x=-\infty}^\infty \delta^{(n)} (x) f(x) dx &= \underbrace{\sum_k^{n-1} \left[ (-1)^k \delta^{(k)}(x) f^{(n-k)}(x) \right]_{x=-\infty}^\infty}_{f^{(n)}(\pm \infty) = f(\pm \infty)=0} + (-1)^n \int_{x=-\infty}^\infty \delta(x) f^{(n)}(x) dx \\ &= (-1)^n \int_{x=-\infty}^\infty \delta(x) f^{(n)}(x) dx \end{align}\) which we will utilize in our further derivation.

Intermezzo is over.

Continuing with Kramers-Moyal

We now have \(\begin{align} p(x_{t + \tau}) = & \sum_{n=0}^\infty \frac{1}{n!} \int_{X'} \int_{Y} ( y_{t+\tau} - x'_t)^n \ \underbrace{ \partial_{x'}^{n} \left[ \delta(x'_t - x_{t+\tau})\right]}_{?} p(y_{t + \tau} | x'_{t}) \ dy_{t+\tau} \ p(x'_t) dx'_t \\ \end{align}\) which we rearrange to \(\begin{align} p(x_{t + \tau}) = & \sum_{n=0}^\infty \frac{1}{n!} \int_{X'} \partial_{x'}^{n} \left[ \delta(x'_t - x_{t+\tau})\right] \underbrace{\int_{Y} ( y_{t+\tau} - x'_t)^n \ p(y_{t + \tau} | x'_{t}) \ dy_{t+\tau}}_{M^{(n)}(x'_t)} \ p(x'_t) dx'_t \\ = & \sum_{n=0}^\infty \frac{1}{n!} \underbrace{ \int_{X'} \underbrace{ \partial_{x'}^{n} \left[ \delta(x'_t - x_{t+\tau})\right]}_{u'(x)} \underbrace{M^{(n)}(x'_t) \ p(x'_t)}_{v(x)} dx'_t }_{\text{Integration by Parts with Dirac delta function}} \\ = & \sum_{n=0}^\infty \frac{1}{n!} (-1)^n \int_{X'} \delta(x'_t - x_{t+\tau}) \partial_{x'}^{n} \left[ M^{(n)}(x'_t) \ p(x'_t) \right] dx'_t\\ \end{align}\)

The delta function \(\delta(x'_t - x_{t+\tau})\) is only one if the values of the two \(x\)’s is the same irrespective of time. It thus serves as a selector which reduces to the integral over the domain \(X'\) to a single evaluation at the numerical value of \(x_{t+\tau}\). So we get the following sum which we expand up to the second order \(\begin{align} p(x_{t + \tau}) = & \sum_{n=0}^\infty \frac{1}{n!} (-1)^n \partial_{x}^{n} \left[ M^{(n)}(x_t) \ p(x_t) \right]\\ = & p(x_t) - \partial_{x} \left[ M^{(1)}(x_t) \ p(x_t) \right] + \frac{1}{2} \partial_{x}^2 \left[ M^{(2)}(x_t) \ p(x_t) \right] + \mathcal{O}(n^3)\\ \end{align}\) where the $n=0$ eliminates most of the operators in the first summand. Pulling \(p(x_t)\) to the left side and finding that the change between \(p(x_{t+\tau})\) and \(p(x_t)\) should be proportional to \(\partial_t p(x_t) \tau\) for a small step size \(\tau\) analogously to an Euler discretization, we obtain \(\begin{align} p(x_{t+\tau}) - p(x_t) = & \partial_t p(x_t) \tau \\ \frac{p(x_{t+\tau}) - p(x_t)}{\tau} = & \partial_t p(x_t). \end{align}\)

Finally we can note that we can could cut off the Taylor expansion after the second order and realize that Taylor expansion is equivalent to the time derivative in the limit of time, i.e. \(\lim_{\tau \rightarrow 0}\) and we can proclaim that \(\begin{align} \partial_t p(x_t) = & - \partial_{x_t} \left[ M^{(1)}(x_t) p(x_t) \right] + \frac{1}{2} \partial_{x_t}^2 \left[M^{(2)}(x_t) p(x_t) \right] \\ = & - \partial_{x_t} \left[ \mu(x_t) p(x_t) \right] + \frac{1}{2} \partial_{x_t}^2 \left[ \sigma^2(x_t) p(x_t) \right] \\ \end{align}\)

Backward Equation

The Kolmogorov backward equation (KBE) can be derived in the same way while paying attention to the derivatives.

In the Kolmogorov forward equation the differential operators \(M^{(n)}\) were defined for for stochastic variables following the natural arrow of time. For the backward expansion of \(p(x_t | x'_{t'})\) we will use differential operators on \(x'_{t'}\). We thus have the ordering of time \(t' \leq t' + \tau \leq t\).

Again we start with the Chapman-Kolmogorov equation and insert an intermediate variable \(x''_{t+\tau}\): \(\begin{align} p(x_t | x'_t) = \int p(x_t | x''_{t'+\tau}) p(x''_{t'+\tau} | x'_{t'}) dx''_{t'+\tau} \end{align}\)

We expand the transition probability \(p(x''_{t'+\tau} | x'_{t'})\) again with a Dirac function \(\begin{align} p(x''_{t'+\tau} | x'_{t'}) = \int \delta(y_{t'+\tau} - x''_{t'+\tau}) p(y_{t'+\tau} | x'_{t'}) dy_{t'+\tau} \end{align}\)

Then we expand the Dirac function with the Taylor series just as in the Forward Kolmogorov equation to obtain \(\begin{align} \delta(y_{t'+\tau} - x''_{t'+\tau}) = & \delta( y_{t'+\tau} - x'_{t'} + x'_{t'} - x''_{t'+\tau}) \\ = & \sum_{n=0}^\infty \frac{1}{n!} (y_{t' + \tau} - x'_{t'})^n \ \partial_{x'}^n \ \delta(x'_{t'} - x''_{t'+\tau}) \end{align}\)

Plugging the expanded Dirac function back into the transition probability we obtain \(\begin{align} p(x''_{t'+\tau} | x'_{t'}) = & \int \delta(y_{t'+\tau} - x''_{t'+\tau}) p(y_{t'+\tau} | x_{t'}) dy_{t+\tau} \\ = & \int \sum_{n=0}^\infty \frac{1}{n!} (y_{t' + \tau} - x'_{t'})^n \ \partial_{x'}^n \ \delta(x'_{t'} - x''_{t'+\tau}) p(y_{t'+\tau} | x_{t}) dy_{t'+\tau} \\ = & \sum_{n=0}^\infty \frac{1}{n!} \partial_{x'}^n \ \delta(x'_{t'} - x''_{t'+\tau}) \int (y_{t' + \tau} - x'_t)^n p(y_{t'+\tau} | x_{t'}) dy_{t'+\tau} \\ = & \sum_{n=0}^\infty \frac{1}{n!} \partial_{x'}^n \ \delta(x'_{t'} - x''_{t'+\tau}) M^{(n)}(x'_{t'}) \\ \end{align}\)

We now plug in the Taylor expansion to substitute \(p(x''_{t'+\tau} | x'_{t'})\) in our original master equation and get \(\begin{align} p(x_t | x'_t) &= \int p(x_t | x''_{t'+\tau}) p(x''_{t'+\tau} | x'_{t'}) dx''_{t'+\tau} \\ &= \int p(x_t | x''_{t'+\tau}) \sum_{n=0}^\infty \frac{1}{n!} \partial_{x'}^n \ \delta(x'_{t'} - x''_{t'+\tau}) M^{(n)}(x'_{t'}) dx''_{t'+\tau} \\ &= \sum_{n=0}^\infty \frac{1}{n!} M^{(n)}(x'_{t'}) \int p(x_t | x''_{t'+\tau}) \partial_{x'}^n \ \delta(x'_{t'} - x''_{t'+\tau}) dx''_{t'+\tau} \\ \end{align}\) where we pulled out the \(n\) and the \(M^{(n)}(x'_{t'})\) as they are independent of the integral over \(x''_{t'+\tau}\). Given our derivation of the KFE, we would be quick to reapply integration by parts, but it turns out that the distribution inside the integral doesn’t contain \(x'_{t'}\) and therefore we can pull the derivative out of the integral. Since a Dirac delta function inside an integral is just a selector, we eliminate the integral and obtain \(\begin{align} p(x_t | x'_t) &= \sum_{n=0}^\infty \frac{1}{n!} M^{(n)}(x'_{t'}) \ \partial_{x'}^n \int p(x_t | x''_{t'+\tau}) \ \delta(x'_{t'} - x''_{t'+\tau}) dx''_{t'+\tau} \\ &= \sum_{n=0}^\infty \frac{1}{n!} M^{(n)}(x'_{t'}) \ \partial_{x'}^n p(x_t | x'_{t'+\tau}) \\ \end{align}\)

Expanding the sum up to the second order \(\begin{align} p(x_t | x'_t) &= p(x_t | x'_{t'+\tau}) + M^{(1)}(x'_{t'}) \ \partial_{x'} p(x_t | x'_{t'+\tau}) + \frac{1}{2} M^{(2)}(x'_{t'}) \ \partial_{x'}^2 p(x_t | x'_{t'+\tau}) \\ \end{align}\) and taking the limit of \(\tau \rightarrow 0\) while discretizing it a la Euler, we get \(\begin{align} p(x_t | x'_t) - p(x_t | x'_{t'+\tau}) &= M^{(1)}(x'_{t'}) \ \partial_{x'} p(x_t | x'_{t'+\tau}) + \frac{1}{2} M^{(2)}(x'_{t'}) \ \partial_{x'}^2 p(x_t | x'_{t'+\tau}) \\ - (p(x_t | x'_{t'+\tau}) - p(x_t | x'_t)) &= M^{(1)}(x'_{t'}) \ \partial_{x'} p(x_t | x'_{t'}) \ \tau + \frac{1}{2} M^{(2)}(x'_{t'}) \ \partial_{x'}^2 p(x_t | x'_{t'}) \ \tau \\ \end{align}\) and by dividing by \(\tau\), we finally get \(\begin{align} - \frac{p(x_t | x'_{t'+\tau}) - p(x_t | x'_t)}{\tau} &= - \partial_{x'} p(x_t | x'_{t'}) \\ &= M^{(1)}(x'_{t'}) \ \partial_{x'} p(x_t | x'_{t'}) + \frac{1}{2} M^{(2)}(x'_{t'}) \ \partial_{x'}^2 p(x_t | x'_{t'}) \\ &= \mu(x'_{t'}) \ \partial_{x'} p(x_t | x'_{t'}) + \frac{1}{2} \sigma^2(x'_{t'}) \ \partial_{x'}^2 p(x_t | x'_{t'}) \\ \end{align}\) which tells us how the probability distribution \(p(x_t | x'_{t'})\) changes as we move further backwards in time.