Fokker, Planck & Ito

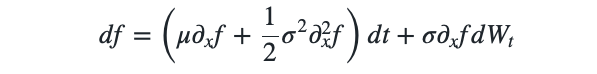
\(\newcommand{\Efunc}[1]{\mathbb{E}\left[ #1\right]} \newcommand{\Vfunc}[1]{\mathbb{V}\left[ #1\right]} \newcommand{\KL}[2]{\text{KL}\left[ #1 \ || \ #2 \right]} \newcommand{\denom}[1]{\frac{1}{#1}} \newcommand{\drift}{\mu(X_t, t)} \newcommand{\diff}{\sigma(X_t, t)}\)

A Dutch, a German and a Japanese walk into a bar …

Let us consider the random variable \(X_t\) that follows an Ito drift-diffusion process of the form \(\begin{align} dX_t = \drift dt + \diff dW_t \end{align}\) where \(W_t\) is a Wiener process with \(W_t \sim \mathcal{N}(0, t)\).

We want to study an arbitrary function \(f(X_t)\) with a compact support, meaning that \(f(X_t)=0, X_t \in \{ -\infty, \infty \}\). Intuitively, this means that for the extreme values of \(\pm \infty\) the function \(f(X_t)\) evaluates to zero. The function \(f(X_t)\) should be twice differentiable in its argument \(X_t\) such that we can use the Taylor expansion up to the second order, giving us \(\begin{align} df = \partial_x f(X_t) dX_t + \denom{2} \partial_x^2 f(X_t) dX_t^2. \end{align}\)

For the infinitissimal values \(dt\), any term with an exponent higher than one will go towards zero at a faster rate. Thus the terms \(dt^2\), \(dt dW_t = dt^{1.5}\) will evaluate to zero at the limit. We can then plug in the dynamics of \(X_t\) to obtain \(\begin{align} df(X_t) = & \partial_x f(X_t) dX_t + \denom{2} \partial_x^2 f(X_t) dX_t^2 \\ = & \partial_x f(X_t) \left( \drift dt + \diff dW_t \right) + \denom{2} \partial_x^2 f(X_t) \left(\drift dt + \diff dW_t \right)^2 \\ = & \partial_x f(X_t) \left( \drift dt + \diff dW_t \right) \\ & + \denom{2} \partial_x^2 f(X_t) \big( \drift^2 \underbrace{dt^2}_{=0} + \drift \diff \underbrace{ dt \ dW_t}_{=0} + \diff^2 \underbrace{dW_t^2}_{=dt} \big) \\ = &\left(\drift \partial_x f(X_t) + \denom{2} \diff^2 \partial_x^2 f(X_t) \right) dt + \diff \partial_x f(X_t) dW_t \end{align}\)

We can abbreviate the notation to enable a higher degree of notational brevity and write \(\begin{align} df = \left( \mu \partial_x f + \denom{2} \sigma^2 \partial_x^2 f \right) dt + \sigma \partial_x f dW_t \end{align}\) which is identical to the line above but shorter and less cluttered.

We can easily see that the differential \(df\) follows an Ito drift-diffusion process, although with modified drift and diffusion terms in direct comparison to \(dX_t\). Naturally we can take the expectation of to isolate the drift of \(df\) since \(\Efunc{dW_t}=0\) by definition, \(\begin{align} \Efunc{df} & = \Efunc{ \mu \partial_x f + \denom{2} \sigma^2 \partial_x^2 f } dt \\ \frac{d}{dt} \Efunc{f} & = \Efunc{ \mu \partial_x f + \denom{2} \sigma^2 \partial_x^2 f } \end{align}\)

Since the Wiener process \(W_t\) introduces stochasticity into the evolution of \(X_t\), we are in fact dealing with a distribution \(p(x, t)\). We can then proceed by plugging in the distribution \(p(x, t)\) into the expectation and writing it out in its full glory, \(\begin{align} \frac{d}{dt} \Efunc{f} & = \Efunc{ \mu \partial_x f + \denom{2} \sigma^2 \partial_x^2 f } \\ &= \int_{-\infty}^\infty \left( \mu \partial_x f + \denom{2} \sigma^2 \partial_x^2 f \right) p(x, t) dx \\ &= \int_{-\infty}^\infty \mu \ \partial_x f \ p(x, t) dx + \denom{2} \int_{-\infty}^\infty \sigma^2 \ \partial_x^2 f \ p(x, t) dx \end{align}\)

The state so far is that we reduced the expected change in \(f\) to two integrals which we now have to solve. For this we can utilize integration by parts which is the sort of the anti derivative of the product rule. Remember that \(\begin{align} \partial_x \left[ u(x) v(x) \right] = \partial_x \left[ u(x) \right] v(x) + u(x) \partial_x \left[ v(x) \right] \end{align}\) or in a easier form \(\begin{align} \left( u(x) v(x) \right)' = u'(x) v(x) + u(x) v'(x) \end{align}\) The integration by parts rule states that for a range \(x \in [ a, b ]\) \(\begin{align} \left[ u(x) v(x) \right]_a^b = \int_a^b u'(x) v(x) dx + \int_a^b u(x) v'(x) dx \end{align}\) or alternatively \(\begin{align} \int_a^b u(x) v'(x) dx = \left[ u(x) v(x) \right]_a^b - \int_a^b u'(x) v(x) dx + \end{align}\)

We can now proceed to identify the relevant terms \(u(x)\) and \(v(x)\) in the two integrals, \(\begin{align} \frac{d}{dt} \Efunc{f} = & \int_{-\infty}^\infty \underbrace{\mu \ p(x, t)}_{u(x)} \ \underbrace{\partial_x f}_{v'(x)} dx + \denom{2} \int_{-\infty}^\infty \underbrace{ \sigma^2 \ p(x, t)}_{u(x)} \ \underbrace{\partial_x^2 f}_{v (x)} dx \\ = & \underbrace{\left[ \mu \ p(x, t) \ f \right]_{-\infty}^\infty}_{=0} - \int_{-\infty}^\infty \partial_x \left[ \mu \ p(x, t) \right] \ f \ dx \\ & + \denom{2} \underbrace{\left[ \sigma^2 \ p(x, t) \ \partial_x f \right]_{-\infty}^\infty}_{=0} - \denom{2} \int_{-\infty}^\infty \partial_x \left[ \sigma^2 \ p(x, t) \right] \ \partial_x f \ dx \end{align}\) For any reasonable probability distribution, evaluating \(p(x,t)\) at \(\pm \infty\) evaluates to zero such that the evaluation brackets \(\left[ p(x,t) \ldots \right]_{-\infty}^\infty = 0\). We can then apply the integration by parts a second time on the second integral to obtain \(\begin{align} \frac{d}{dt} \Efunc{f} = & - \int_{-\infty}^\infty \partial_x \left[ \mu \ p(x, t) \right] \ f \ dx - \denom{2} \int_{-\infty}^\infty \underbrace{\partial_x \left[ \sigma^2 \ p(x, t) \right]}_{u(x)} \ \underbrace{\partial_x f}_{v'(x)} \ dx \\ = & \int_{-\infty}^\infty \partial_x \left[ \mu \ p(x, t) \right] \ f \ dx \\ & - \denom{2} \underbrace{\left[ \partial_x \left[ \sigma^2 \ p(x, t) \right] \ f \right]_{-\infty}^\infty}_{=0} + \denom{2} \int_{-\infty}^\infty \partial_x^2 \left[ \sigma^2 \ p(x, t) \right] \ f \ dx \\ = & \int_{-\infty}^\infty f \left( - \partial_x \left[ \mu \ p(x, t) \right] + \denom{2} \partial_x^2 \left[ \sigma^2 \ p(x, t) \right] \right) dx \end{align}\) With Leibniz’ rule we can pull in the time derivative on the left hand side to obtain \(\begin{align} \frac{d}{dt} \Efunc{f} = & \frac{d}{dt} \int_{-\infty}^\infty f(x) p(x,t) dx \\ =& \int_{-\infty}^\infty f(x) \ \partial_t \ p(x,t) dx \end{align}\) which gives us \(\begin{align} \int_{-\infty}^\infty f(x) \ \partial_t \ p(x,t) dx = \int_{-\infty}^\infty f \left( - \partial_x \left[ \mu \ p(x, t) \right] + \denom{2} \partial_x^2 \left[ \sigma^2 \ p(x, t) \right] \right) dx \end{align}\) The last step to obtain the Fokker-Planck equation is to observe that the function \(f\) which is integrated over occurs both on the left and the right hand side. Since the integrals \(\int f(x) \ldots dx\) is identical on both sides we can equate the derivatives directly to obtain \(\begin{align} \partial_t \ p(x,t) = - \partial_x \left[ \mu \ p(x, t) \right] + \denom{2} \partial_x^2 \left[ \sigma^2 \ p(x, t) \right] \end{align}\) which is the Fokker-Planck equation!