04 Feb 2025

Discrete Diffusion from First Principles

Diffusion, ODEs and Expressing One with the Other

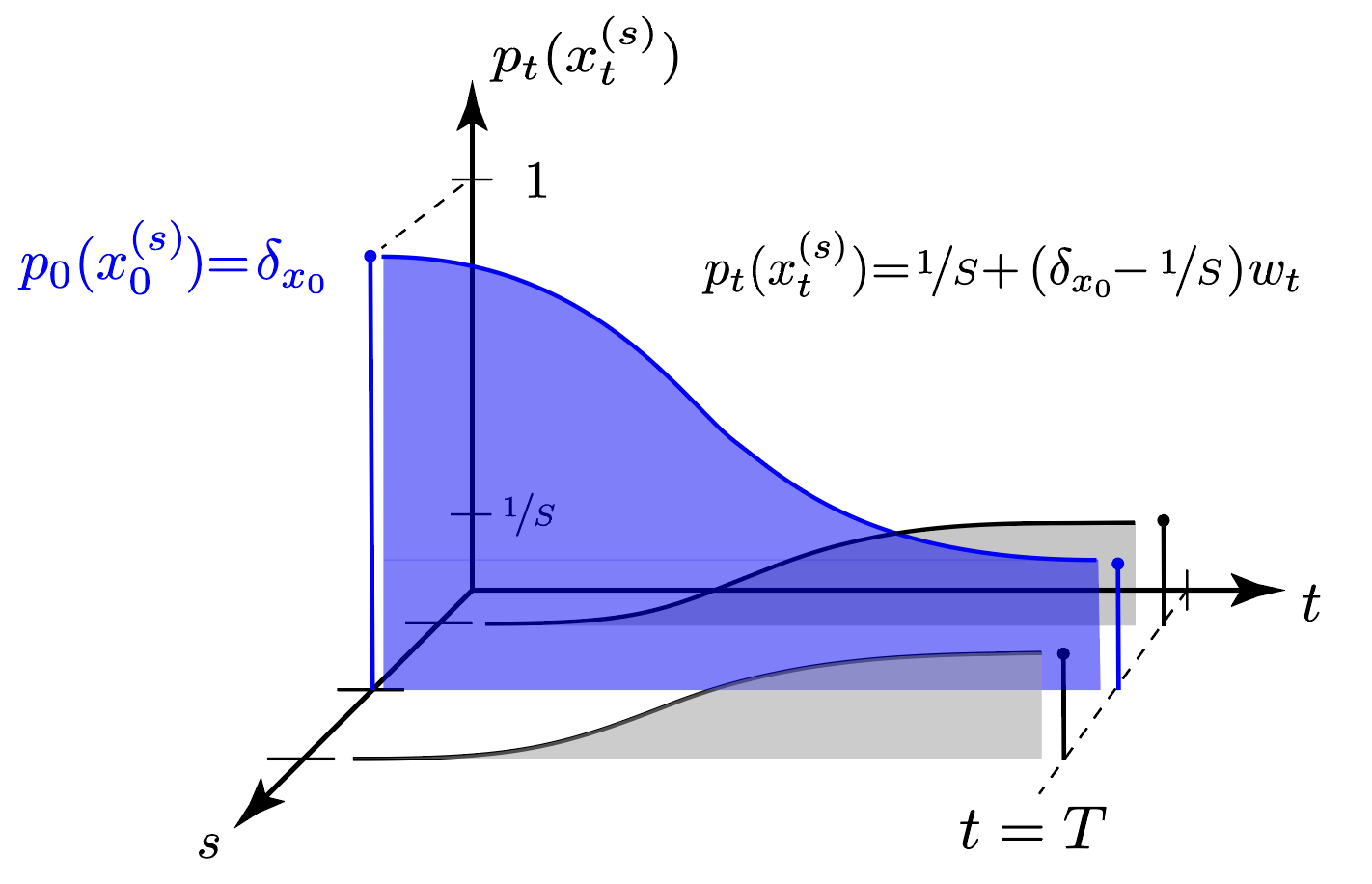
Binary Diffusion

Let us have a stochastic process ${X(t): 0 \leq t \leq 1 }$. The random variable $X(t)$, which we shall abbreviate as $X_t$ can take on only two states with $X_t \in \{-1, +1\}^D$.

The stochastic process of $X_t$ has marginal distributions in time, namely $p_t(x)$. The marginal distribution assigns probabilities to two possible states at time $t$, namely $p_t(x=-1)$ and $p_t(x=+1)$. In order to keep the notation succinct, we will abbreviate the positive and negative states with a raised index $^+$ and $^-$. We can then write $x^+_t$ for a positive state at time $t$ and $x^-_t$ for a negative state with the corresponding marginal probabilities $p^\pm_t(x_t)$.

In a time-reversible Markov Jump Processes with only two states, we have two rates: the forward rate $r_t^+(x^+_t|x^-_t)$ and the backward rate $r_t^-(x^-_t|x^+_t)$. The rates $r^+$ and $r^-$ denote the propensity of switching the state going from $x^+_t$ to $x^-_t$ and vice-versa.

Time reversibility implies that any transition is reversible, thus we have

$$ \begin{align} p_{t|t+\Delta t}(x^-_t|x^+_t) \ p_{t}(x^+_t) = p_{t+\Delta t|t}(x^+_t|x^-_t) \ p_t(x^-_t) \end{align} $$

All that the equation above states is that residing in state $x^+_t$ with probability $p_{t}(x^+_t)$ and moving to $x^-_t$ should equal the probability of moving in the reverse direction $x^-_t \rightarrow x^+_t$. If this equation wouldn’t hold, simulating the process forward in time would in the long run yield a different marginal distribution than simulating the process backward in time. Essential we would deal with two different stochastic processes instead with a single time-reversible one. This property is called detailed balance and is essential for time reversible stochastic processes and is pivotal for MCMC sampling for example.

Applying the limit to the time difference $\lim_{\Delta t \rightarrow 0}$, we will obtain the instantaneous rate $r^+_t$.

$$ \begin{align} \lim_{\Delta t \rightarrow 0} p_{t|t+\Delta t}(x^-_t|x^+_t) p_{t}(x^+_t) &= \lim_{\Delta t \rightarrow 0} p_{t+\Delta t|t}(x^+_t|x^-_t) p_t(x^-_t) \\ r^-_t(x^-_t|x^+_t) p(x^+_t) &= r^+_t(x^+_t|x^-_t) p(x^-_t). \end{align} $$

For the two rates $r^+_t$ and $r^-_t$ and the respective marginal distributions $p_t(x^+_t)$ and $p_t(x^-_t)$ we want the following equation to hold

$$ \begin{align} r^-_t(x^-_t|x^+_t) p_t(x^+_t) = r^+(x^+_t | x^-_t) p_t(x^-_t). \end{align} $$

The Forward Process

In fact we can also infer something about the marginal distribution in the forward direction. The marginal probability of a certain state over time is really just the previous marginal distribution where we subtract from it the probability of moving out of the state and add the probability of moving into the state. $\begin{align} p_{t+ \Delta t} (x^+_t) =p_{t}(x^+_t) - p_{t+\Delta t| t}(x^-_t|x^+_t) p_{t}(x^+_t) + p_{t+\Delta t| t}(x^+_t|x^-_t) p_{t}(x^-_t) \end{align}$

In the continuous time limit, we saw that we can express the transition probability $p_t(x^+_t | x^-_t)$ with its instantaneous counterpart, the jump rate $r$. While the jump rate is instantaneous, the transition probability is the probability of moving from $x^+_t$ to $x^-_t$ in a small time interval $\Delta t$. Therefore, we can express the transition probability as a product of the rate and the time difference. In essence, this is a bit like an euler integration of a differential equation where we multiply the rate of change with the time difference to obtain the change in the variable. $\begin{align} p_{t+ \Delta t} (x^+_t) &= p_{t}(x^+_t) - p_{t+\Delta t| t}(x^-_t|x^+_t) \ p_{t}(x^+_t) \ + p_{t+\Delta t| t}(x^+_t|x^-_t) \ p_{t}(x^-_t) \\ &= p_{t}(x^+_t) - r^-_t(x^-_t|x^+_t) \ \Delta t \ p_{t}(x^+_t) \ + r^+_t(x^+_t|x^-_t) \ \Delta t \ \ p_{t}(x^-_t) \\ \end{align}$

In fact, we can obtain an ordinary differential equation of the marginal by rearranging the terms and taking the limit of the time difference to zero:

$\begin{align} p_{t+ \Delta t} (x^+_t) &= p_{t}(x^+_t) - r^-_t(x^-_t|x^+_t) \ \Delta t \ p_{t}(x^+_t) \ + r^+_t(x^+_t|x^-_t) \ \Delta t \ \ p_{t}(x^-_t) \\ \frac{p_{t+ \Delta t} (x^+_t) - p_{t}(x^+_t)}{\Delta t} &= - r^-_t(x^-_t|x^+_t) \ p_{t}(x^+_t) \ + r^+_t(x^+_t|x^-_t) \ p_{t}(x^-_t) \\ \partial_t \ p_{t}(x^+_t) &= - r^-_t(x^-_t|x^+_t) \ p_{t}(x^+_t) \ + r^+_t(x^+_t|x^-_t) \ p_{t}(x^-_t) \\ \end{align}$

One of the core pillars of diffusion models is that the forward process is tractable and allows for an analytical solution. So instead of choosing a complicated, state dependent rate $r^+(x^+_t|x^-_t)$ and $r^-(x^-_t|x^+_t)$, we choose a simple, time-dependent rate $\beta_t$.

In order to not make the notation too verbose, we will switch to a simpler notation ($p_t(x^+_t) = p^+_t$) and introduce $\beta_t$ to our master equation, $\begin{align} \dot{p}_t^+ &= - \beta_t \ p^+_{t} \ + \beta_t \ p^-_{t}. \end{align}$

For discrete states, we can exploit the knowledge that the sum of all probabilities over all states is equal to one, i.e. $\sum_{x} p_t(x) = 1$. $\begin{align} \dot{p}_t^+ &= - \beta_t \ p^+_{t} \ + \beta_t \ p^-_{t} \quad \quad \quad | \quad p^-_{t} = 1 - p^+_{t} \\ &= - \beta_t \ p^+_{t} \ + \beta_t \ (1- p^+_{t}) \\ &= - \beta_t \ (2 p^+_{t} - 1) \\ &= - 2 \beta_t \ (p^+_{t} - \frac{1}{2}) \end{align}$ which oddly enough looks like the deterministic part of an Ornstein-Uhlenbeck process $dX_T = - \theta ( X_t - \mu) dt + \sigma dW_t$.

We can then proceed to solve the ODE for the marginal distribution $p^+_t$ by using the solution of the OU process. $\begin{align} p^+_t | p^+_0 = p^+_0 e^{\left(-2 \int_0^t \beta(\tau) d\tau \right)} + \frac{1}{2} \left(1 - e^{\left(-2 \int_0^t \beta(\tau) d\tau \right)} \right) \end{align}$

The term $e^{\left(-2 \int_0^t \beta(\tau) d\tau \right)}$ can only take on values between 0 and 1, and thus acts as a weighting function. We can then rewrite the solution of the marginal distribution in terms of a weighting function $w_t = e^{\left(-2 \int_0^t \beta(\tau) d\tau \right)}$, $\begin{align} p^+_t | p^+_0 = p^+_0 w_t + \frac{1}{2} \left(1 - w_t \right) \end{align}$

We can now proceed to calculate the expected value of $X_t$ over time, $\begin{align} \mu_t &= \mathbb{E}_{p_t}[x_t] \\ &= x^+_t \cdot p^+_t + x^-_t \cdot p^-_t \\ &= (+1) \cdot p^+_t + (-1) \cdot p^-_t \\ &= p^+_t - p^-_t \quad \quad \quad | p^-_t = 1 - p^+_t \\ &= p^+_t - (1 - p^+_t) \\ &= 2 p^+_t - 1 \\ &= 2 \left( p^+_0 w_t + \frac{1}{2} \left(1 - w_t \right) \right) - 1 \\ &= 2 p^+_0 w_t + 1 - w_t - 1 \\ &= \underbrace{\left(2 p^+_0 -1 \right)}_{\in \{-1, +1\}} w_t \\ &= x_0 \ w_t \\ &= x_0 \ e^{\left(-2 \int_0^t \beta(\tau) d\tau \right)} \\ \end{align}$

We can also solve for the solution of the expected value directly by solving the ODE for $\mu_t$, $\begin{align} \mu_t &= \mathbb{E}_{p_t}[x_t] \\ &= x^+_t \cdot p^+_t + x^-_t \cdot p^-_t \\ &= (+1) \cdot p^+_t + (-1) \cdot p^-_t \\ &= p^+_t - p^-_t \quad \quad \quad | \quad p^-_t = 1 - p^+_t \\ &= p^+_t - (1 - p^+_t) \\ &= 2 p^+_t - 1 \\ \end{align}$

Taking the time derivative $\dot{\mu}_t$ of $\mu_t$ we can express it’s solution via the rate $\beta_t$, $\begin{align} \dot{\mu}_t &= \partial_t \left[ 2 p^+_t - 1 \right]\\ &= 2 \dot{p}^+_t \\ &= 2 (- 2 \beta_t \ (p^+_{t} - \frac{1}{2}) ) \\ &= -4 \beta_t \ (p^+_{t} - \frac{1}{2}) \\ &= -4 \beta_t \ (p^+_{t} - \frac{1}{2}) \\ &= -4 \beta_t \ \underbrace{p^+_{t}}_{= \frac{1}{2} (\mu_t + 1)} - 2 \beta_t \\ &= -2 \beta_t \ (\mu_t + 1) - 2 \beta_t \\ &= -2 \beta_t \ \mu_t \\ \end{align}$

Solving the ODE above yields the solution for $\mu_t$, $\begin{align} \dot{\mu}_t &= -2 \beta_t \ \mu_t \\ \frac{d\mu_t}{\mu_t} &= -2 \beta_t \\ d \log \mu_t &= -2 \beta_t \quad \quad \quad | \int_0^t \cdot \ d\tau \\ \left[ \log \mu_t \right]_{t=0}^{t} &= \int_0^t -2 \beta_\tau d\tau \\ \log \mu_t - \log \mu_0 &= \int_0^t -2 \beta_\tau d\tau \\ \log \frac{\mu_t}{\mu_0} &= \int_0^t -2 \beta_\tau d\tau \\ \frac{\mu_t}{\mu_0} &= \exp\left(\int_0^t -2 \beta_\tau d\tau \right) \\ \mu_t &= \mu_0 \exp\left(\int_0^t -2 \beta_\tau d\tau \right) \\ &= \mu_0 \ w_t \\ &= x_0 \ w_t \\ \end{align}$

where $\mu_0$ is the initial condition and depends on the initial value $x_0 \in {-1, +1}$.

This concludes our solution of the forward process for a binary variable. Given an initial sample $x_0$ and the state change rate $\beta_t$, we can compute the probability of observing $x^+_t$ or $x^-_t$ at any point in time $t$.

The Reverse Process

Further up, we saw the detailed balance requirement for a time-reversible stochastic process dictates the relationship between the jump rates. While solving the forward process, we only considered the forward rates.

Here, we will derive the correct reverse rates. But first, let’s revisit the detailed balance equation for the reverse process and extrac the reverse rate, $\begin{align} r^-_t(x^-_t|x^+_t) p_t(x^+_t) &= r^+(x^+_t | x^-_t) p_t(x^-_t) \\ r^-_t(x^-_t|x^+_t) &= \frac{p_t(x^-_t)}{p_t(x^+_t)}r^+(x^+_t | x^-_t) \\ &= \frac{p_t(x^-_t)}{p_t(x^+_t)} \beta_t \end{align}$

Normally, we could simply plug in the marginal probabilities $p_t(x^-_t)$ and $p_t(x^+_t)$ and the rate $\beta_t$ to obtain the reverse rate. But for the reverse process, the idea is not to sample already existing data $x_0$, but to generate new data from noise. Thus we need to express the reverse rate somehow differently.

It turns out that we can express the reverse rate in terms of a conditional expectation $p_{0|t}(x_0|x_t)$ and the solution of the forward process, $\begin{align} \frac{p_t(x^-_t)}{p_t(x^+_t)} &= \frac{\sum_{x_0} p_t(x^-_t|x_0) p(x_0)}{p_t(x^+_t)} \\ &= \frac{\sum_{x_0} p_t(x^-_t|x_0) p(x_0)}{p_t(x^+_t)} \frac{p_{t|0}(x^+_t | x_0)}{p_{t|0}(x^+_t | x_0)} \\ &= \frac{\sum_{x_0} p_t(x^-_t|x_0) }{p_t(x^+_t | x_0)} \frac{p_{t|0}(x^+_t | x_0) p(x_0)}{p_{t|0}(x^+_t)} \\ &= \sum_{x_0} \frac{p_t(x^-_t|x_0) }{p_t(x^+_t | x_0)} p_{0|t}(x_0 | x^+_t) \\ &= \mathbb{E}_{p_{0|t}(x_0 | x^+_t)}\left[ \frac{p_t(x^-_t|x_0) }{p_t(x^+_t | x_0)} \right] \end{align}$

In the binary case we can easily express $p_t^-$ in terms of it’s reciprocal $p_t^+$, $\begin{align} \frac{p_t(x^-_t)}{p_t(x^+_t)} &= \mathbb{E}_{p_{0|t}(x_0 | x^+_t)}\left[ \frac{p_t(x^-_t|x_0) }{p_t(x^+_t | x_0)} \right] \\ &= \mathbb{E}_{p_{0|t}(x_0 | x^+_t)}\left[ \frac{1 - p_t(x^+_t|x_0) }{p_t(x^+_t | x_0)} \right] \\ &= \mathbb{E}_{p_{0|t}(x_0 | x^+_t)}\left[ \frac{1}{p_t(x^+_t | x_0)} - 1 \right] \quad \quad | \quad (30): p_t^+ = \frac{1}{2}(1 + \mu_t) \\ &= \mathbb{E}_{p_{0|t}(x_0 | x^+_t)}\left[ \frac{2}{1 + \mu_t} - 1 \right] \\ &= \mathbb{E}_{p_{0|t}(x_0 | x^+_t)}\left[ \frac{2}{1 + \mu_t} - 1 \right] \\ &= \mathbb{E}_{p_{0|t}(x_0 | x^+_t)}\left[ \frac{2}{1 + x_0 w_t} - 1 \right] \\ \end{align}$

In fact we can generalize this ratio algebraically for any move by incorporating the current $x_t$ as the sign of the denominator. This can be easily checked by expressing $\mu_t$ in terms of $p^-_t$ in equation (28) and calculating both ratios $p^-_t/p^+_t$ and $p^+_t/p^-_t$ which differ only by a sign in the denominator.

Thus we get $\begin{align} r(x_t) &= \mathbb{E}_{p_{0|t}(x_0 | x^+_t)}\left[ \frac{2}{1 + x_t x_0 w_t} - 1 \right] \\ \end{align}$

which is the expectation of a nonlinear function of $x_0$. This poses a problem because we can’t pull in readily the expectation into the fraction.

But there is a trick we can apply to simplify the expression. Since $x_0$ can only take on two distinct states $x_0 \in {-1, +1}$, we can linearize the fraction, like so

$$ \begin{align} \frac{2}{1 + x_t x_0 w_t} = A + x_t x_0 B \end{align} $$

Since $x_t x_0 = \pm 1$ we can evaluate those two cases and get

$$ \begin{align} x_t x_0 = - 1: \quad \frac{2}{1 + w_t} &= A + B \\ x_t x_0 = + 1: \quad \frac{2}{1 - w_t} &= A - B \\ \end{align} $$

Solving this gives us

$$ \begin{align} A &= \frac{2}{1 - w_t^2} \\ B &= \frac{-2w_t}{1 - w_t^2} \end{align} $$

which let’s us factorize the entire thing to

$$ \begin{align} r(x_t) &= \mathbb{E}_{x_0|x_t} \left[ \frac{2}{1 + x_t x_0 w(t)} -1 \right] \\ &= \mathbb{E}_{x_0|x_t} \left[ A + x_t x_0 B -1 \right] \\ &= \mathbb{E}_{x_0|x_t} \left[ \frac{2 (1 - w(t) x_t x_0)}{1 - w(t)^2} -1 \right] \\ &= 2 \frac{ 1 - w(t) \ x_t \ \mathbb{E}_{x_0|x_t} \left[x_0 \right]}{1 - w(t)^2} -1 \\ \end{align} $$

This effectively gives us a denoising objective $\mathbb{E}_{x_0|x_t} [ x_0 ]$ which is the initial condition of our jump process that would have generated $x_t$.

Categorical Diffusion

This can be extended to a finite state setup with $S > 2$ states with

$$ \begin{align} p_i(t + dt) = p_i(t) \left( 1 - \sum_{j \neq i} \lambda_{i\rightarrow j} \ dt \right) + \sum_{j \neq i} p_{j}(t) \ \lambda_{j \rightarrow i} dt \end{align} $$

with the first term summing up all outgoing transitions and the second summing all incoming probability mass. In effect, we simplify the state transition from a $S$-way state transition to a two way transition of one versus any other state.

In classical diffusion fashion, we determine the forward process rates $\lambda$ with a shared noising rate $\beta(t)$ and obtain

$$ \begin{align} p_i(t + dt) &= p_i(t) \underbrace{ \left(1 - \sum_{j \neq i} \beta(t) dt \right)}_{\text{outflow}} + \underbrace{ \beta(t) \sum_{j \neq i} p_{j}(t) dt}_{\text{inflow}} \\ &= p_i(t) \left(1 - (S-1) \beta(t) dt \right) + \beta(t) \underbrace{\sum_{j \neq i} p_{j}(t)}_{1-p_i(t)} dt \\ &= p_i(t) \left(1 - (S-1) \beta(t) dt \right) + \beta(t) (1-p_i(t)) dt \\ \end{align} $$

where $\sum_{j \neq i} \beta(t) = (S-1) \beta(t)$. Taking the time derivative gives us

$$ \begin{align} \dot{p}_i(t) &= - \beta(t) (S -1 ) p_i(t) + \beta(t) (1 - p_i(t)) \\ &= \beta(t) \big\{ -(S -1 ) p_i(t) + 1 - p_i(t) \big\} \\ &= \beta(t) \big\{ -S p_i(t) + p_i(t) + 1 - p_i(t) \big\} \\ &= \beta(t) \big\{ 1 -S p_i(t) \big\} \\ &= - S \beta(t) \big\{p_i(t) \frac{1}{S} \big\} \end{align} $$

To solve this ordinary differential equation, we will work with the substitution $u(t) = \beta(t) (1 - S p(t))$,

$$ \begin{align} u(t) &= \beta(t) (1 - S p(t)) \\ \dot{u}(t) &= - \beta(t) \ S \ \dot{p}(t)\\ \dot{p}(t) &= - \frac{1}{\beta(t) S} \dot{u}(t) = \beta(t) (1 - S p(t)) = u(t) \\ u(t) &= - \frac{1}{\beta(t) S} \dot{u}(t) \\ u(t) &= - \frac{1}{\beta(t) S} \frac{d u(t)}{d t} \\ - \beta(t) S dt &= \frac{d u(t)}{u(t)} \\ - S \int_0^t \beta(\tau) d\tau &= \int_0^t d \log u(\tau) \\ - S \int_0^t \beta(\tau) d\tau &= \left[ \log u(\tau) \right]_{\tau=0}^t \\ - S \int_0^t \beta(\tau) d\tau &= \log \frac{u(t)}{u(0)} \\ u(0) \exp \left[ - S \int_0^t \beta(\tau) d\tau \right] &= u(t) \end{align} $$

plugging $u(t)$ back in gives us

$$ \begin{align} \beta(t) (1 - S p(t)) &= \beta(t) (1 - S p(0)) \exp \left[ - S \int_0^t \beta(\tau) d\tau \right] \\ 1 - S p(t) &= (1 - S p(0)) \exp \left[ - S \int_0^t \beta(\tau) d\tau \right] \\ p(t) &= \frac{1}{S} - \left( \frac{1}{S} - p(0) \right) \exp \left[ - S \int_0^t \beta(\tau) d\tau \right] \\ p(t) &= \frac{1}{S} + \left( p(0) - \frac{1}{S} \right) \underbrace{\exp \left[ - S \int_0^t \beta(\tau) d\tau \right]}_{\text{exponential interpolator}} \end{align} $$

which yields a nice exponential interpolation between $\frac{1}{S}, \beta(t) \gg 0$ at equilibrium and $p(0), \beta(0)=0$.

This is identical to the binary Ising case, where we rescaled the states from ${0,1}$ to ${-1, +1}$ with $2 \cdot x -1$. In the Ising case, the equilibrium was 0 which is in the middle of ${-1, +1}$ and not $\frac{1}{2}$ as for ${0, 1}$.

Backward Rates

We now aim to work with data with $D$ dimensions and $S$ states, $x_t \in \mathbb{R}^{D \times S}$.

For each discrete state of the process we obtain the forward process of

$$ \begin{align} p_i(t) = \frac{1}{S} + \left( p_i(0) - \frac{1}{S} \right) \exp \left[ - S \int_0^t \beta(\tau) d\tau \right] \end{align} $$

where $p_i(0)$ is a one hot discrete distribution.

We have the backward rate defined as

$$ \begin{align} f^-_t(y|x) &= \frac{p_t(y)}{p_t(x)} f^+_t(x|y) \\ &= \mathbb{E}_{x_0 | x_t}\left[ \frac{p_t(y|x_0) }{p_t(x|x_0)} \right] f^+_t(x|y) \end{align} $$

with which we can condition our backward ratio on a data set of $x_0$’s

For the backward rate we require two probabilities in the ratio $p_t(y|x_0) / p_t(x|x_0)$ conditioned on the same data sample $x_0$, which we can compute readily via

$$ \begin{align} p_t(x_t | x_0) = \frac{1}{S} + \left( p(x_0) - \frac{1}{S} \right) \exp \left[ - S \int_0^t \beta(\tau) d\tau \right] \end{align} $$

with $p(x_0)$ being a discrete, one-hot distribution with $S$ bins in $D$ dimensions. The noising process $p_t(x_t| x_0)$ can be evaluated readily with the equation above.

Multi-Class ODE

Going from $i$ to $j$ with the ratio with $w_t = \exp( - S \int_{\tau=0}^t \beta(\tau) d\tau)$

Since we have only three combinations of variables, we can solve the system of linear equations in the following

$$ \begin{align} \delta_{i, x_0} = \delta_{j, x_0} = 0 : & \quad r_{ij}(x_0) = \frac{\frac{1}{S} - w_t \frac{1}{S}}{\frac{1}{S} - w_t \frac{1}{S}} = 1 = A\\ \delta_{i, x_0} = 1, \delta_{j, x_0} = 0 : & \quad r_{ij}(x_0) = \frac{\frac{1}{S} - w_t \frac{1}{S}}{\frac{1}{S} + w_t( 1 - \frac{1}{S})} = A + B \\ \delta_{i, x_0} = 0, \delta_{j, x_0} = 1 : & \quad r_{ij}(x_0) = \frac{\frac{1}{S} + w_t(1 - \frac{1}{S})}{\frac{1}{S} - w_t \frac{1}{S}} = A + C \\ \end{align} $$

Plugging in the solution gives us

$$ \begin{align} r_{ij}(x_0) &= \frac{p(x_t = j | x_0)}{p(x_t = i | x_0)} \\ &= \frac{\frac{1}{S} + w_t( \delta_{j, x_0} - \frac{1}{S})}{\frac{1}{S} + w_t( \delta_{i, x_0} - \frac{1}{S})} \\ &= A + \delta_{i, x_0} \ B + \delta_{k, x_0} \ C \\ &= 1 + \underbrace{\left( \frac{\frac{1}{S} - w_t \frac{1}{S}}{\frac{1}{S} + w_t( 1 - \frac{1}{S})} -1 \right) \delta_{i, x_0}}_{\text{staying rate}} + \underbrace{\left( \frac{\frac{1}{S} + w_t(1 - \frac{1}{S})}{\frac{1}{S} - w_t \frac{1}{S}} -1 \right) \delta_{j, x_0}}_{\text{switching rate}} \end{align} $$

For large $t$, the diffusion rate $\beta_t$ will be concurrently large, while $\lim_{t \rightarrow 0} \rightarrow 1$, such that the switching rate becomes larger and larger for incorrect states. This necessitates how to design the function $w_t$.

Tweaking the Diffusion Function $w_t$

The weighting function $w_t$ is defined as

$$ \begin{align} w_t &= \exp( - S \int_{\tau=0}^t \beta(\tau) d\tau) \\ &= \exp( -S \ \beta(t)) \end{align} $$

which is data independent and can be chosen freely.

For starters, I propose to use for $t \in [0, 1]$

$$ \begin{align} w_t = \frac{1}{2}\left( 1 + \cos(\pi t) \right) \end{align} $$

which is a cosine weighting function with ‘flattened’ edges (flattens out at $t=0$ and $t=1$ via a shifting and scaling).

We can then deduce $\beta_t$ as

$$ \begin{align} \beta_t = - \frac{1}{S}\log \left[ \frac{1}{2}\left( 1 + \cos(\pi t) \right) \right] \end{align} $$

We can see that the diffusion rate $\beta_t$ is directly scaled with the number of states, such that for more states $S$ the diffusion rate is reduce as there is intrinsically more variance due to more possibilities of state switching.

Secondly, we would like to regularize the weighting function to a range $w_t \in [w_{min}/(S-1), (1 - w_{min}) \cdot \delta_{i,0}]$, where we bound the weighting of the true state $i$ at time $t=0$ to $1- w_{min}$ and distribute the remaining probability $w_{min}$ onto the $S-1$ remaining states,

$$ \begin{align} p_t(x_t=i | x_0) &= \frac{1}{S} + \left( \delta_{i,0} - \frac{1}{S} \right) w_t \underbrace{- \left( w_{min} \ \delta_{i,0} + \frac{w_{\min}}{S-1} ( 1 - \delta_{i,0}) \right) w_t}_{\text{state switching regularization}} \\ &=\frac{1}{S} + \left( ( 1 - w_{min}) \delta_{i,0} - \frac{1}{S} + \frac{w_{\min}}{S-1} ( 1 - \delta_{i,0}) \right) w_t \end{align} $$

During optimization, this state switching regularization might be unimportant, but during sampling, this might provide an important regularization to prevent exploding state switching rates at $t \approx 0$.

While the equation above characterize a smooth function, we can for simplicity’s sake also bound the function with a floor and a ceiling by restricting $w_t$ to $w_t \in [ \frac{w_{min}}{S-1}, 1 - w_{min} ]$. There only difference is that the weighting function is not smooth anymore, which should be of little importance to the prediction task during sampling.