Annealed Importance Sampling

Boltzmann Distribution

In statistical mechanics, a system can take on different states $x_i$ and every possible state (or “microstate”) of a system is assigned an energy value, $E_i$. Intuitively, states with lower energy are more likely to occur, while those with higher energy are less likely. This relationship is physically intuitive: you expect a soccer ball to be more likely to be found at the bottom of a hill than at the top, because it takes energy to roll it uphill. Hold a tennis ball in your hand and drop it. It will fall to the ground, because the gravitational potential energy is lower at the ground than in your hand. Boil a pot of water, then turn off the heat. The water will eventually cool down as the water tries to reach thermal equilibrium with its surroundings. The water “system” will dissipate heat to its environment in order to reach a state of lower energy.

However, the precise relationship between energy and probability is not obvious at first glance.

In order to be rigorous (whatever that means on a blog like this that is written in my freetime), we will also have to introduce the notion of average energy. It’s a common misconception that the total energy of a system is always fixed. In statistical mechanics, we often consider systems that can exchange energy with their environment (for example, a pot of water cooling down in a room). In such cases, the system’s energy fluctuates due to interactions with its surroundings. What is typically fixed is the average energy over many realizations or samples, not the energy of any single microstate. This is why, when deriving the Boltzmann distribution, we impose a constraint on the expected (average) energy $\langle E \rangle = \sum p(x) E(x)$, rather than the total energy itself. This approach allows us to model systems at thermal equilibrium, where the energy can vary from one microstate to another, but the average remains constant.

To make this connection, we seek a probability distribution over states that reflects our physical intuition: low-energy states should be favored, but there should still be a nonzero chance of observing higher-energy states, for example especially at higher temperatures. The question is: how do we assign probabilities to states, given their energies, in a principled way?

The answer comes from the maximum entropy principle: among all possible probability distributions consistent with our knowledge (such as the average energy), we choose the one with the largest entropy. This ensures we are not making any unwarranted assumptions beyond what is known. The result of this maximization is the Boltzmann distribution, which connects the energy of a state to its probability of being observed.

We should remember that the logarithm of small values are large and negative, while the logarithm of large values are small and positive. The entropy of a probability distribution $p$ computes the expected surprise of observing a state $x$ with probability $p(x)$:

With only knowledge of the energies $E_i$ of the states, we would like to find a probability distribution $p_i$ that maximizes the entropy $S[p]$ while satisfying certain constraints, such as normalization and a fixed average energy. The entropy maximization arises from the principle of maximum entropy, which states that we should choose the probability distribution that has the highest entropy among all distributions that satisfy our constraints. That’s because the only thing we know about the system is the energy, and we want to avoid making any additional assumptions.

Secondly, we want to ensure that the probabilities are normalized and that the average energy matches a given value. This leads us to the following constraints:

• Normalization: $\sum_x p(x) = 1$
• Fixed average energy: $\sum_x p(x) E(x)) = \langle E \rangle$

Next, we can use the method of Lagrange multipliers to incorporate these constraints into our optimization problem. We introduce Lagrange multipliers $\alpha$ and $\beta$ for the normalization and average energy constraints, respectively.

To find the optimal probability distribution $p_i$, we need to maximize the Lagrangian $L$ with respect to $p(x)$. This involves taking the derivative of $L$ with respect to $p(x)$ and setting it to zero.

Rearranging this equation gives us the expression for the probability distribution:

where $\alpha$ is a/any/some constant that does not depend on $i$.

It is important to note that the sign of the Lagrange multiplier $\beta$ in the exponent is not arbitrary. In principle, one might wonder why we choose $-\beta E(x)$ rather than $+\beta E(x)$ in the Boltzmann distribution. If we were to use $+\beta E(x)$, the resulting probability distribution would assign higher probabilities to higher-energy states, which contradicts both physical intuition and the requirement that the distribution be normalizable. Specifically, for many systems, the sum or integral $\sum_x \exp(\beta E(x))$ would diverge (as it would keep increasing for states with absurdly large energies), making it impossible to normalize the distribution and thus violating the basic property of a probability distribution.

By choosing $-\beta E(x)$, we ensure that higher-energy states are exponentially suppressed, and the partition function $Z = \sum_x \exp(-\beta E(x))$ converges for physically meaningful energy functions. This guarantees that the Boltzmann distribution is a proper, normalizable probability distribution, consistent with both the maximum entropy principle and the laws of thermodynamics.

This shows that the probability of each state is proportional to the exponential of its negative energy, scaled by constants determined by the constraints.

where $Z$ is the partition function that ensures normalization, and $\beta$ is a constant that can be interpreted as the inverse temperature (in physics, $\beta = \frac{1}{kT}$, where $k$ is Boltzmann’s constant and $T$ is the temperature).

This is the Boltzmann distribution.

Energy

In both statistical mechanics and machine learning, the concept of energy provides a way to quantify the “preference” for different states or configurations. In physics, the energy of a system describes its physical state, while in machine learning, energy can be interpreted as a measure of how well a model fits the data—lower energy corresponds to a better fit.

However, it is important to recognize that the absolute value of energy is not meaningful; only differences in energy between states matter. For example, in physics, potential energy is often defined relative to the Earth’s surface, but we could also measure the potential energy from the point of all the dead people in the ground six feet under. Then we would add six feet of potential energy to every state in the system, effectively shifting the reference point for potential energy. But shifting this reference point (such as adding a constant to all energy values) would simply increase the energy of the entire system without changing the relative differences between states. This is known as the gauge invariance of energy.

This property means that we can always add or subtract a constant $c$ to the energy of every state in a system without changing the resulting probabilities. The Boltzmann distribution, which assigns probabilities to states based on their energies, is invariant to such shifts because the normalization constant (the partition function $Z$) absorbs the change. Suppose we shift the energy function by a constant $c$, so $E’(x) = E(x) + c$. The Boltzmann distribution becomes:

The new normalization constant is:

Therefore,

Thus, adding a constant $c$ to the energy does not change the resulting probability distribution; the effect is fully absorbed by the normalization constant $Z$. As a result, two energy functions that differ only by a constant offset will yield the same probability distribution over states.

When working with models, it is tempting to focus directly on energy values, since lower energy indicates a better fit. However, absolute energy values are not interpretable without a reference point. For instance, if you are given energy values of 100, 200, 300, and 400, it is unclear what these numbers mean in isolation. In contrast, if you are given probabilities of 0.01, 0.02, 0.03, and 0.04, their meaning is immediately clear: they represent the likelihood of each state. Said differently, since the probabilities are normalized you implicitly compare them to all other existing energies values through the partition function $Z = \sum \exp(-\beta E(x))$ which by definition incorporates all other states. The probability allows you to make claims about the relationship of a single energy with respect to all other energies.

Technically, you could try to find the minimum energy state and then subtract that value from all energies, but this is not always practical or necessary. In many cases, we are more interested in the relative differences between states rather than their absolute energy values. This is why, in practice, we prefer to work with probabilities rather than raw energy values.

The conversion from energy to probability is accomplished using the Boltzmann distribution: $P(x) = \frac{e^{-E(x)}}{Z}$, where $Z$ is the partition function that ensures normalization. In machine learning, this principle appears in functions like logsumexp and softmax, where adding a constant to all log-likelihoods does not change the resulting probabilities.

By the way, the softmax is a Boltzmann distribution with a temperature of 1. The log softmax function is defined as:

where $x_i$ are the input values. This is equivalent to the Boltzmann distribution.

We can test this property in practice by using the softmax function in PyTorch. and run two softmax functions with one input shifted by a constant:

import torch
x = torch.randn(4)
torch.nn.functional.softmax(x, dim=0), torch.nn.functional.softmax(x+100, dim=0)

which should return the same two probability distributions.

This property is often exploited to improve numerical stability during computation, as it allows us to shift energy or log-likelihood values without affecting the model’s predictions. A common numerical trick when computing the log-sum-exp (logsumexp) function is to subtract the maximum value from all inputs before exponentiating. This does not change the resulting probabilities, since adding or subtracting a constant from all energies (or logits) is absorbed by the normalization. However, it greatly improves numerical stability by ensuring that the largest exponent is $\exp(0) = 1$, preventing overflow. The logsumexp is computed as:

This transformation ensures that all values in the exponential function $x_i - \max_i(x)<=0$, which prevents overflow and maintains numerical stability. The final result is the same as if we had computed the log-sum-exp without the shift, but it avoids potential issues with large exponentials. Again, we can see that the absolute values of the energies (or logits) do not matter; we can add and subtract constants without changing the final probabilities.

Temperature

In 2008, Katy Perry famously declared that it’s ‘Hot ‘n Cold’. It turns out that the concept of temperature is actually way more involved. In fact, if you check Wikipedia, you will find that the definition of temperature is actually quite complicated and involves statistical mechanics, thermodynamics, and even quantum mechanics.

Above, we’ve seen that the Boltzmann distribution is given by:

where $\beta$ is a constant that can be interpreted as the inverse temperature.

and usually, the factor $\beta$ is defined as $\beta = \frac{1}{kT}$, where $k$ is Boltzmann’s constant and $T$ is the temperature in Kelvin. Thus for higher temperature, the more uniform the distribution becomes, and for lower temperature, the more peaked it becomes around the lowest energy states.

But how do we connect the temperature to the previously defined Lagrangian multiplier $\beta$? For that we have to explore both the entropy $S[p]$ as a function of the Boltzman distribution $p$ and the partition function $Z$. The entropy of the Boltzmann distribution is given by:

It was completely new to me that the temperature is in fact not a physical quantity, but rather a mathematical construct that arises from thermodynamics. The temperature is the differential coefficient in the form of

where $S$ is the entropy and $U$ is the expected energy.

So the temperature $T$ actually is the derivative of the entropy with respect to the expected energy $U = \mathbb{E}_p[E]$. It tells us by what amount the entropy of the system increases or decreases if we add or subtract energy. There is naturally a certain disconnect of how temperature is defined in a thermodynamic sense and how we experience it as humans. Particularly the reciprocal coefficient $1/T$ is somewhat counterintuitive but actually makes a lot of sense.

A little though experiment …

The best example I could think of was water at a the phase transitions of ice to water and water to gas. For that we will look at the number of positions the water atoms can take inside an ice cube and inside a liquid. For this visual example, we define entropy as the number of positions the water atoms can take according to Boltzmann $S = \log \Omega$. We divvy up the ice cube and the liquid into many, many small cells in the respective three dimensions and count whether each of these cells is occupied by a water molecule or not.

We put an ice cube into a pan, we start adding energy to our water molecules by turning on the stove. At 0 degrees Celsius, they are quite literally frozen in place into a semi-regular grid and the number of states it can assume is actually quite low (because none of the water molecules can move). There is exactly one configuration and combinatorially, a single set of 3D cells is occupied by the water molecules. Since there is only one configurations of the atoms the Boltzman entropy is $S = \log 1 = 0$. Consequentially, the entropy is zero.

Now we increase the expected energy $U$ by adding a bit of heat. Some of the ice melts and suddenly the water molecules are free to move around. Since the water molecules can suddenly move around, they can take fill one of the many 3D cells in the pan (just positions in space since it’s a liquid) They can now be anywhere in the pan thus markedly increasing the entropy (when measured in possible positions in the pan).

Imagine we increased the energy by just right amount to release 5 single water molecules. If we had divided our pan into $10 \times 10$ cells (ignoring the ice cube in the middle of the pan for a moment), they could be in any of these $10 \times 10$ cells that directly touch the surface of the pan. With the binomial coefficient, this gives $\left(\stackrel{100}{5} \right) = 100! / (5! ( 100 - 5)! = 100 \cdot 99 \cdot 98 \cdot 97 \cdot 96 / 120 = 75,287,520$ combinations of where the water molecules could possibly be. Take the logarithm of that and we have the entropy $S = 18.3$. Consequently, the entropy has increased from $0$ to $18.3$ by adding just a bit of energy to release some puny 5 water molecules.

As we’ve increased the entropy significicantly by adding a bit of energy, the differential should be high, which is exactly what the reciprocal term $1/T$ measures. If we add a bit of energy at $T=0.001$, the differential will be $dS/dU = 1,000$. For every bit of energy we add at a low temperature, we release some water molecules to be free to be anywhere in the pan and they go from being at a single position in space to potentially being anywhere in the pan.

But now we keep adding energy by continuing to heat the pan. We release more and more water molecules and the water molecules can be found in more and more cells. But now, we have a lot more water molecules flowing and swirling around between the cells in our grid. One of our $10 \times 10$ cells could be filled by any of the free water molecules. But as we keep adding energy, the number of water molecule configurations (i.e. which cell is occupied by a water molecule) does not increase as much as it did before and thus the entropy increase per unit of temperature starts to slow down.

Obviously, this is a simplified example, but it illustrates the point that the temperature is a measure of how much the entropy changes with respect to energy.

The astute reader will have noticed that the entropy would reach its maximum when exactly half the water molecules are free to move around. After the proverbial half-time break, the entropy would actually decrease again, because the water molecules would be able to move around more freely and thus the number of positions they can take would decrease. If all the water molecules were thawed, there would only be one configuration of the water molecules, namely that they are all in the pan in one specific cell each.

But here our simplefied example breaks down, because we are not considering the fact that the water molecules can actually store energy in their kinetic motion, their rotational and vibrational modes etc. In reality, the entropy would continue to increase as we add more energy. But we only wanted to illustrate the point that the temperature is a measure of how much the entropy changes with respect to energy.

With some idea of how the temperature influences the entropy increase/decrease per unit of energy, we can now connect the temperature to the Boltzmann distribution.

Specifically, we are interested in the relationship between the temperature $T$ and the Lagrange multiplier $\beta$. More specifically, we want to find the derivative $dS/dU$ in terms of $\beta$. The only free variable in our entire setup is the Lagrange multiplier $\beta$, as both $Z=\sum \exp(-\beta E(x))$ and $U = \sum p(x) E(x) = \sum 1/Z \exp(-\beta E(x)) E(x)$ are functions of $\beta$ and $E(x)$ ultimately.

Thus we write out the total derivative of the entropy $S[p]$ with respect to $\beta$:

With a bit more calculus, we can compute the partial derivatives:

which after subtituing in yields:

The relationship of interest is just a step away by observing that

MCMC Sampling

While the Boltzmann distribution provides a principled way to assign probabilities to states based on their energies, actually sampling from it is a major challenge in practice. The difficulty arises because the normalization constant $Z = \sum_x \exp(-\beta E(x))$ is typically intractable to compute for all but the simplest systems. Evaluating $Z$ requires summing or integrating over a large number of states, which quickly becomes computationally prohibitive as the system grows in complexity. As a result, we cannot directly sample from the normalized Boltzmann distribution, and instead must rely on alternative sampling strategies—such as Markov Chain Monte Carlo or importance sampling—that circumvent the need to compute $Z$ explicitly.

The origins of Monte Carlo methods trace back to the Manhattan Project during World War II, where scientists faced the challenge of simulating complex physical processes involved in nuclear reactions. Stanislaw Ulam, while recovering from illness, conceived the idea of using random sampling to solve deterministic problems that were otherwise analytically intractable. Together with John von Neumann and Nicholas Metropolis, Ulam formalized these techniques, naming them “Monte Carlo” after the famous casino, to reflect their reliance on randomness and probability. This approach enabled the efficient estimation of quantities such as neutron diffusion and reaction rates, laying the foundation for modern computational statistics and probabilistic modeling.

When sampling from an unnormalized probability distribution, such as the Boltzmann distribution, our goal is to explore the energy landscape in a way that reflects the physical behavior of real systems. In practice, this means we want to accept moves to states with lower energy (and thus higher probability) much more frequently than moves to higher energy states. Transitions to higher energy states are rare and typically only occur due to significant fluctuations—mirroring the physical intuition that systems tend to settle into low-energy configurations and only occasionally “jump” to higher-energy ones. This principle is at the heart of Markov Chain Monte Carlo (MCMC) methods, which propose random moves across the energy surface, readily accepting transitions to lower energy states while being reluctant to accept (only sometimes) moves to higher energy states. The acceptance mechanism ensures that the sampling process faithfully reproduces the statistical properties of the target distribution, efficiently exploring regions of high probability while suppressing unlikely, high-energy configurations.

A key insight in working with unnormalized probability distributions, such as the Boltzmann distribution, is that the ratio of two distributions removes the partition function. Mathematically, if we have a distributions $\pi(x) = \frac{1}{Z} \tilde{\pi}(x) = \frac{1}{Z} \exp(-\beta E(x))$ and two samples $x$ and $x’$, then their ratio is

The partition functions cancel out, allowing us to work directly with the unnormalized densities. This brings us one step closer to sampling from the Boltzmann distribution without needing to compute the partition function $Z$ explicitly.

Detailed Balance

The principle of detailed balance arises naturally from the physical intuition of how systems explore their energy landscapes. Imagine a particle moving randomly among states: it will gladly transition to a lower energy state $x’$ from a higher energy state $x$, as this is energetically favorable and thus more probable. However, transitions to higher energy states $x$ are less likely from lower energy states $x’$, reflecting the fact that such moves require an input of energy and occur only due to rare fluctuations.

In summary we should define the following terms:

Detailed balance is crucial because it allows the Markov chain to move freely over the energy landscape, exploring all regions without bias, while still respecting the underlying probabilities dictated by the energy differences. This guarantees that the sampling process is both physically meaningful and statistically correct and the four terms above should relate to each other in the following way:

In order to get a functioning sampling algorithm out of the detailed balance equation, Mrs Metropolis and Hasting split the transition probabilities $T(x|x’)$ and $T(x’|x)$ into a proposal step $q$ and an acceptance step $a$.

For simplicities sake we’ll use a symmetric proposal distribution $q(x’|x) = q(x|x’)$. This means that the proposal distribution is the same in both directions, which is often a reasonable assumption in practice. An example would be a isotropic Gaussian distribution centered around the current state $x$ with a fixed standard deviation and we would have $\mathcal{N}(x’|\mu=x, \sigma^2) = \mathcal{N}(x|\mu=x’, \sigma^2)$.

In the symmetric proposal probability case, the acceptance ratio simplifies to

The acceptance probability is $100\%$ if the new state $x’$ has lower energy than the current state $x$, and it is less than $100\%$ if the new state has higher energy. If $\pi(x) < \pi(x’)$, then the acceptance probability is $a(x’|x) = 1$. If the new state $x’$ has higher energy than the current state $x$, then the acceptance probability is less than $100\%$ and given by the ratio $\pi(x’)/\pi(x)$. We thus always accept moves to lower energy states, and we accept moves to higher energy states with a probability that decreases exponentially with the energy difference.

We can in fact check that the proposed sampling algorithm satisfies the detailed balance condition

from which we see that the detailed balance equality still holds true, albeit in a slightly different form.

Importance Sampling

Importance sampling is a technique for estimating expectations under a target distribution $\pi(x)$ when direct sampling is difficult, but sampling from a simpler proposal distribution $q(x)$ is feasible. The key idea is to reweight samples drawn from $q(x)$ so that they reflect the target distribution.

Suppose we want to estimate the partition function $Z$ for the Boltzmann distribution: \(\pi(x) = \frac{1}{Z} e^{-E(x)} = \frac{1}{Z} \tilde{\pi}(x)\)

Directly computing $Z = \int e^{-E(x)} dx$ is often intractable. Instead, we sample $x$ from a proposal distribution $q(x)$ and use the following identity: \(\begin{align} Z &= \int e^{-E(x)} dx \\ &= \int \frac{q(x)}{q(x)} e^{-E(x)} dx \\ &= \int \frac{e^{-E(x)}}{q(x)} q(x) dx \\ &= \int \frac{e^{-E(x)}}{q(x)} dQ(x) \\ &= \mathbb{E}_{x \sim q} \left[ \frac{e^{-E(x)}}{q(x)} \right] \end{align}\)

Here, each sample $x$ from $q(x)$ is assigned a weight $\frac{e^{-E(x)}}{q(x)}$. Averaging these weights over many samples gives an unbiased estimate of $Z$. The effectiveness of importance sampling depends on how well $q(x)$ covers the regions where $e^{-E(x)}$ is large; poor overlap leads to high-variance estimates.

In summary, importance sampling allows us to estimate quantities under a complex target distribution by leveraging samples from a tractable proposal, correcting for the mismatch using importance weights.

Annealed Importance Sampling

In high-dimensional spaces, direct importance sampling often fails due to mode collapse: the proposal distribution $q(x)$ may have little or no overlap with the high-probability regions (modes) of the target distribution $\pi(x)$. As a result, even though importance sampling provides an unbiased estimator for the partition function, it is only effective if the proposal covers all significant modes. If the proposal misses a mode, no amount of reweighting will recover it—the estimator will simply ignore that region.

This raises a natural question: why do we attempt to bridge the gap between the proposal and target distributions in a single step? Instead, we can construct a sequence of intermediate distributions that gradually morph the proposal into the target, allowing the sampler to traverse the energy landscape more smoothly and discover all relevant modes.

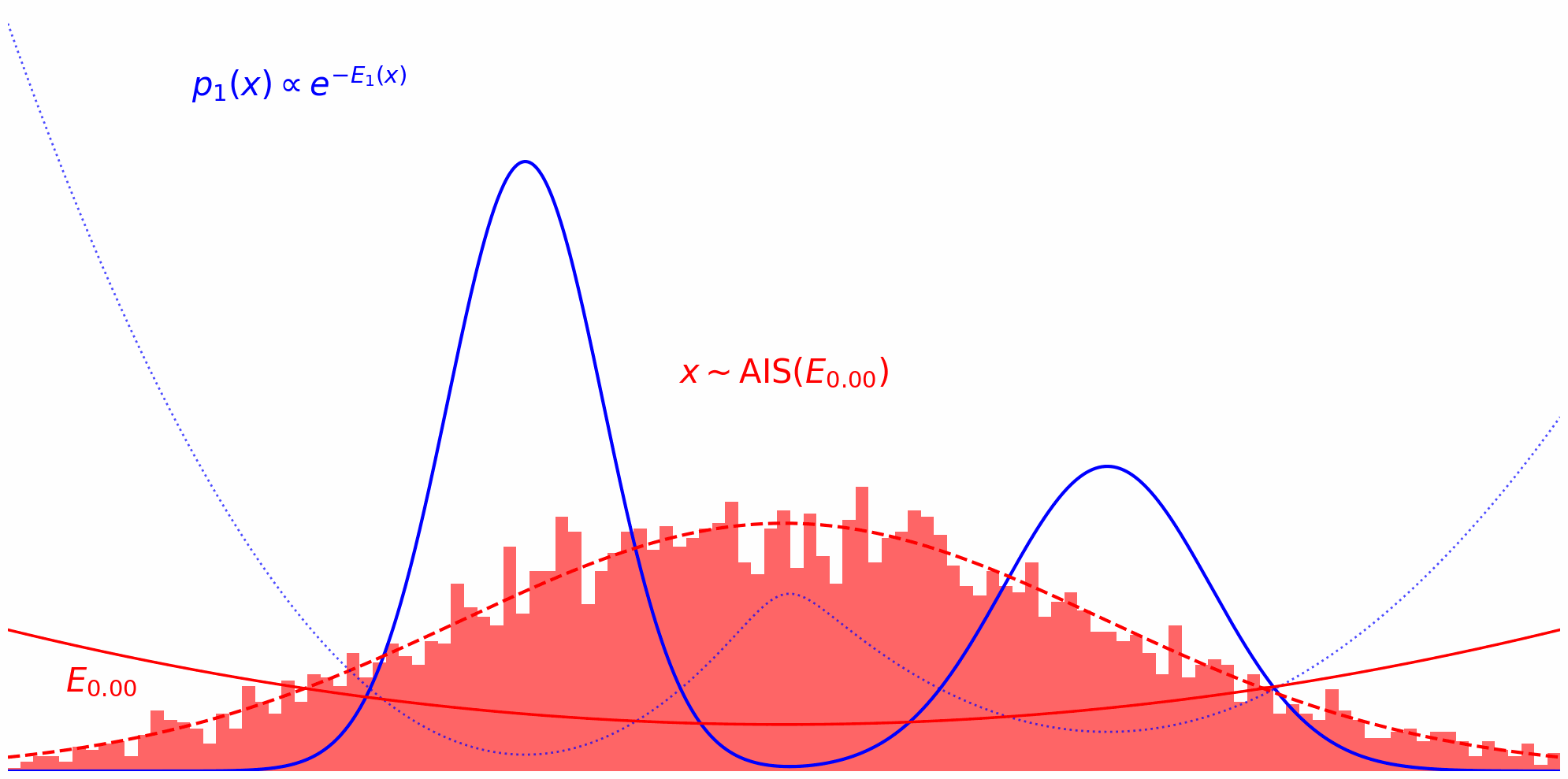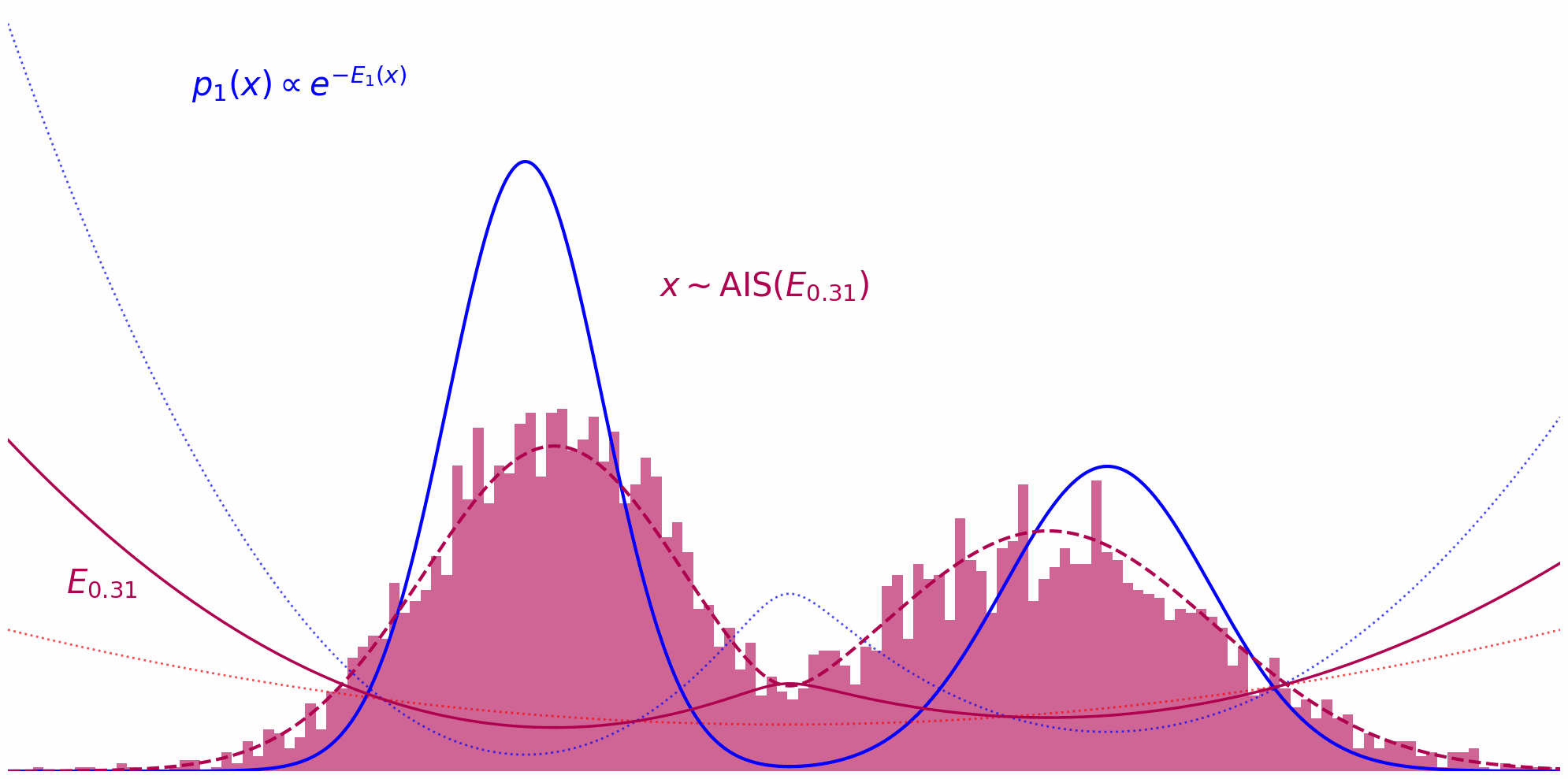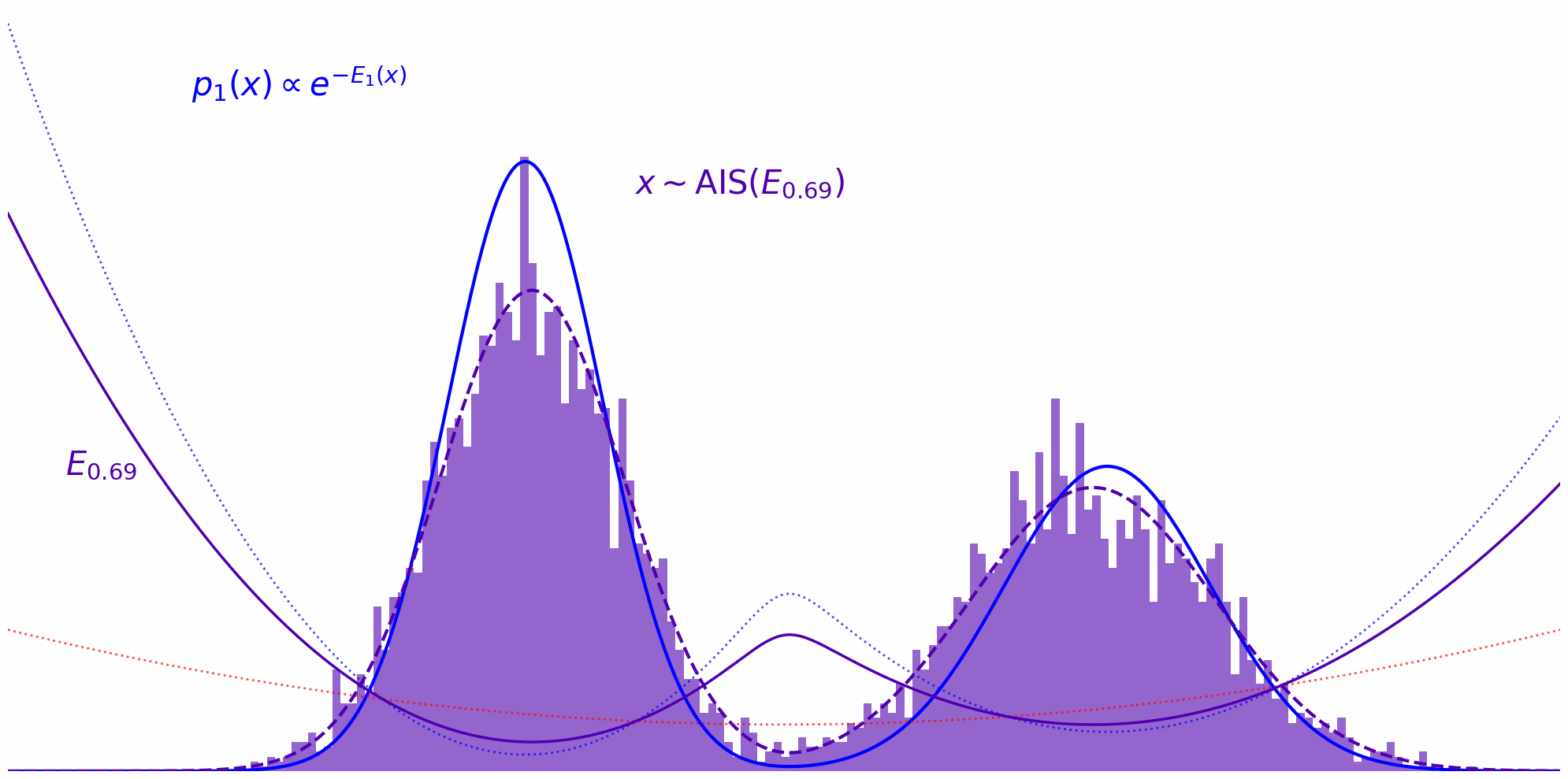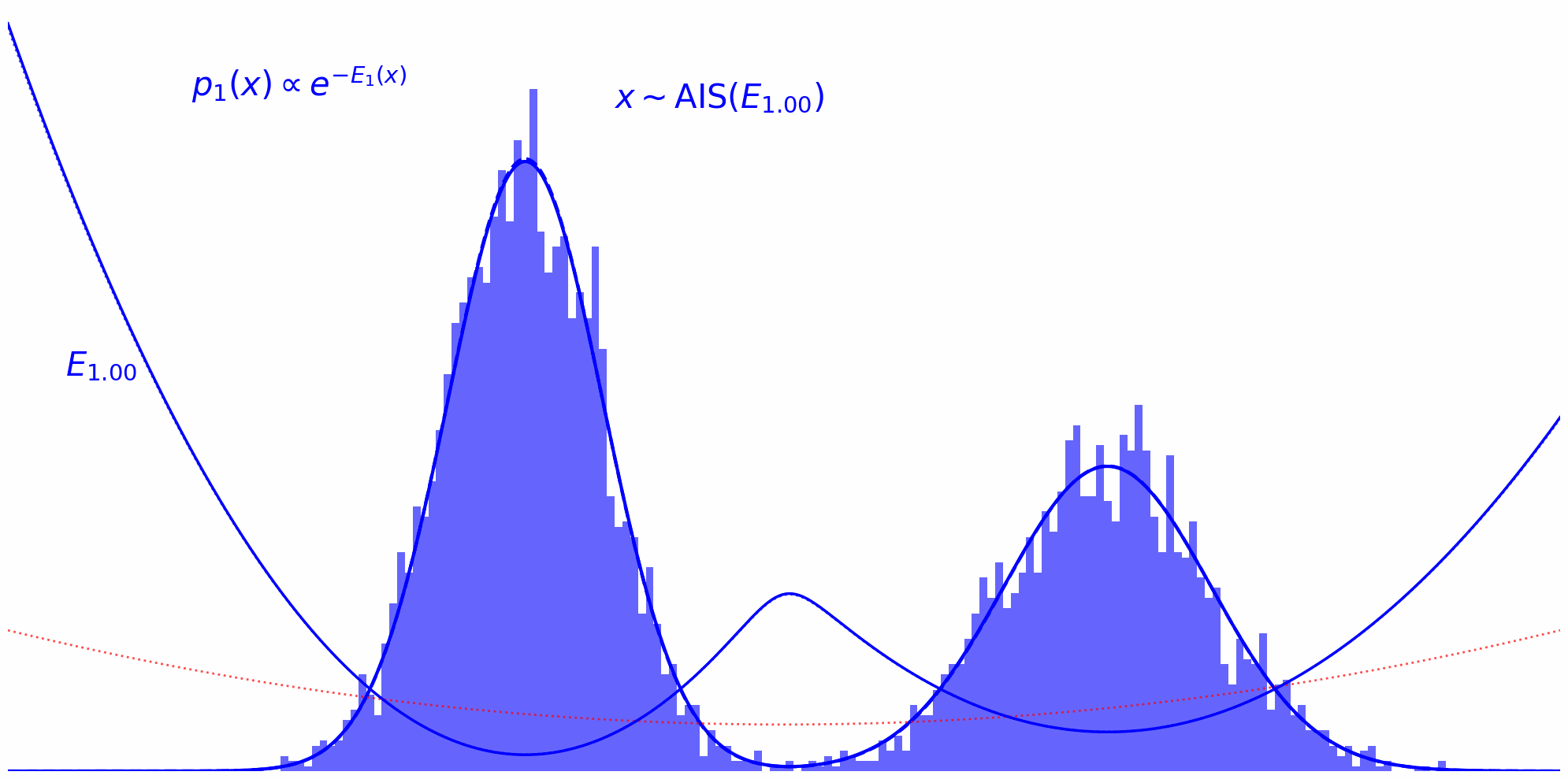
Annealed Importance Sampling (AIS) implements this idea by defining a series of intermediate energy functions that interpolate between the proposal and target. At each stage, we define an unnormalized density: \(\tilde{\pi}_t(x) = \tilde{\pi}_0(x)^{(1-t)} \tilde{\pi}(x)^t\) where $t$ ranges from $0$ (pure proposal) to $1$ (pure target). For example, discretizing $t$ as ${0, 0.33, 0.66, 1}$ yields a sequence of distributions that smoothly transition from proposal to target.

We begin by sampling from the initial proposal distribution $\pi_0(x)$, which could be a broad Gaussian: \(\pi_0(x) = \mathcal{N}(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{1}{2\sigma^2}(x-\mu)^2}\) This distribution is chosen to be easy to sample from and to cover the support of the target.

At each annealing stage, we use the samples from the previous distribution as starting points for an MCMC sampler targeting the next intermediate distribution. For instance, after sampling from $\pi_0$, we run MCMC targeting $\pi_{0.33}$, then use those samples to initialize MCMC for $\pi_{0.66}$, and so on, gradually shifting the energy landscape toward the target.

The partition function for each intermediate distribution can be estimated recursively using importance weights:

At each stage, we repeat the process:

Finally, we reach the target distribution:

By chaining these estimates, we obtain an unbiased estimator for the partition function of the target:

In summary, AIS leverages a sequence of intermediate distributions to guide samples gradually from the proposal to the target, using MCMC at each stage to adaptively explore the energy landscape. This approach mitigates mode collapse and improves the reliability of partition function estimation in challenging, high-dimensional settings. \(\begin{align} \tilde{\pi}_t(x) = \tilde{\pi}_0(x)^{(1-t)} \tilde{\pi}(x)^t \ \end{align}\)

discretize to $t\in {0, 0.33, 0.66, 1 }$.

As the initial distribution $\pi_0$ we can take a standard normal distribution with a large standard deviation $\sigma »1$ \(\begin{align} \pi_0(x) = \mathcal{N}(x; \mu, \sigma^2) = \underbrace{\frac{1}{\sqrt{2\pi \sigma^2}}}_{=Z_0} \overbrace{e^{-\frac{1}{2\sigma^2}(x-\mu)^2}}^{\tilde{\pi}_0} \end{align}\)

We now start with the first annealing step, which is to estimate the partition function $Z_{0.33}$ for the intermediate distribution $\pi_{0.33}(x)$, \(\begin{align} Z_{0.33} &= \int \tilde{\pi}_{0.33} \ dx \\ &= \int \frac{\pi_{0}}{\pi_{0}}\tilde{\pi}_{0.33} \ dx \\ &= \int \frac{\tilde{\pi}_{0.33}}{\pi_{0}} \ d\pi_{0} \\ &= \mathbb{E}_{x_0 \sim \pi_0} \left[ \frac{\tilde{\pi}_{0.33}}{\pi_{0}} \right] \\ &= \mathbb{E}_{x_0 \sim \pi_0} \left[ \frac{\tilde{\pi}_{0.33}}{\frac{1}{Z_0}\tilde{\pi}_{0}} \right] \\ &= Z_0 \ \mathbb{E}_{x_0 \sim \pi_0} \left[ \frac{\tilde{\pi}_{0.33}}{\tilde{\pi}_{0}} \right] \\ & \downarrow\\ \pi_{0.33}(x) &= \frac{1}{Z_{0.33}}\tilde{\pi}_{0.33}(x) \end{align}\)

Having obtained the partition function $Z_{0.33}$, we now have an (approximate) distribution $\pi_{0.33}(x)$ from which we can sample. These samples serve as proposals for the next stage: estimating $Z_{0.66}$ via importance sampling. Specifically, we draw samples from $\pi_{0.33}$ and use them to compute expectations under the intermediate distribution $\pi_{0.66}$, continuing the annealing process.

We can repeat this process for each subsequent step in the annealing schedule. At every stage, the partition function from the previous distribution is propagated forward, allowing us to express the partition function at the current step as a product of the initial partition function and a chain of expected importance weights. Specifically, for any intermediate step $t_k$, we have:

This telescoping structure means that the initial partition function $Z_0$ is “pulled through” all the way to the final target, accumulating the necessary corrections at each stage via the intermediate expectations.

Specifically, we can write the partition function for each step in our little annealing process as follows: \(\begin{align} Z_{0.66}(x) &= \int \tilde{\pi}_{0.66} \ dx \\ &= \mathbb{E}_{x \sim \pi_{0.33}} \left[ \frac{\tilde{\pi}_{0.66}}{\pi_{0.33}} \right] \\ &= \mathbb{E}_{x \sim \pi_{0.33}} \left[ \frac{\tilde{\pi}_{0.66}}{\frac{1}{Z_{0.33}}\tilde{\pi}_{0.33}} \right] \\ &= Z_{0.33} \ \mathbb{E}_{x \sim \pi_{0.33}} \left[ \frac{\tilde{\pi}_{0.66}}{\tilde{\pi}_{0.33}} \right] \\ &= Z_0 \ \mathbb{E}_{x_0 \sim \pi_0} \left[ \frac{\tilde{\pi}_{0.33}}{\pi_{0}} \right] \mathbb{E}_{x \sim \pi_{0.33}} \left[ \frac{\tilde{\pi}_{0.66}}{\tilde{\pi}_{0.33}} \right] \\ Z_{1}(x) &= \int \tilde{\pi}_{1} \ dx \\ &= \mathbb{E}_{x \sim \pi_{0.66}} \left[ \frac{\tilde{\pi}_{1}}{\pi_{0.66}} \right] \\ &= \mathbb{E}_{x \sim \pi_{0.66}} \left[ \frac{\tilde{\pi}_{1}}{\frac{1}{Z_{0.66}}\tilde{\pi}_{0.66}} \right] \\ &= Z_{0.66} \ \mathbb{E}_{x \sim \pi_{0.66}} \left[ \frac{\tilde{\pi}_{1}}{\tilde{\pi}_{0.66}} \right] \\ &= Z_0 \ \mathbb{E}_{x_0 \sim \pi_0} \left[ \frac{\tilde{\pi}_{0.33}}{\pi_{0}} \right] \mathbb{E}_{x \sim \pi_{0.33}} \left[ \frac{\tilde{\pi}_{0.66}}{\tilde{\pi}_{0.33}} \right] \ \mathbb{E}_{x \sim \pi_{0.66}} \left[ \frac{\tilde{\pi}_{1}}{\tilde{\pi}_{0.66}} \right] \\ \end{align}\)

It’s tempting to think we can simply multiply the expectations at each annealing stage as if the samples are independent. However, this is not the case—and it’s a subtle but important point. The initial samples from $\pi_0$ only assign probability mass to regions they actually visit. If those samples miss significant regions of the target distribution, subsequent stages cannot recover them, no matter how many samples we draw later. This means that the coverage of the initial proposal is crucial: if a mode is missed early, it remains inaccessible throughout the annealing process. Thus, the reliability of AIS depends not just on the number of samples, but on their ability to explore all relevant regions of the energy landscape from the very beginning.

But all is not lost. Instead of relying solely on “simple” importance sampling, we can run full MCMC chains targeting each intermediate energy function. We begin with samples $x_0$ from $\pi_0$ and use them to initialize an MCMC chain targeting $\pi_{0.33}$. After sufficient sampling, we obtain representative samples $x_{0.33}$ from $\pi_{0.33}$. These samples then serve as starting points for an MCMC chain targeting $\pi_{0.66}$, and after enough steps, we have samples $x_{0.66}$ distributed according to $\pi_{0.66}$. This process continues recursively, with each stage’s samples initializing the next chain, until we reach $x_1$—samples from the final target distribution. This approach ensures that each intermediate distribution is properly explored, improving coverage and reducing the risk of missing important modes.

By leveraging MCMC at each annealing stage, AIS can adaptively traverse the energy landscape, allowing samples to migrate between modes that would otherwise be inaccessible in a single-step importance sampling scheme. This staged approach helps mitigate the risk of mode collapse and ensures that the final samples better represent the target distribution. In practice, the choice of annealing schedule (the sequence of $t$ values) and the number of MCMC steps per stage are critical hyperparameters that balance computational cost against the quality of partition function estimates and sample diversity.

The whole thing in action can be observed down below. Here, we’re running MCMC on each interpolation level $t$ and reuse the thus obtained samples on the next level $t+\Delta t$:

AIS is widely used in machine learning for estimating partition functions of complex models, such as Restricted Boltzmann Machines and energy-based models, where direct computation is infeasible. Its combination of importance weighting and staged MCMC sampling makes it a powerful tool for tackling high-dimensional inference problems.

In fact, this approach has been directly implemented as a machine learning algorithm in the paper Stochastic Normalizing Flows, which leverages annealed importance sampling and MCMC transitions to improve sample diversity and partition function estimation in high-dimensional models. In that paper, the normalizing flow layers do the approximate distribution of probability mass. You can imagine it as the invertible flow layers moving probability mass approximately (sort of like proposing initial samples) and the stochastic MCMC layers refining the samples by exploring the energy landscape more thoroughly. The MCMC samples don’t require any parameters in their transition probabilities, at least in their straight forward implemention so they are very cheap to compute. The authors propose a novel approach to normalizing flows that incorporates annealed importance sampling to improve the quality of samples generated from complex distributions. By using MCMC transitions between flow layers, they can effectively explore the energy landscape and ensure that the final samples are representative of the target distribution. This method allows for more efficient training of generative models and better estimates of partition functions, making it a valuable contribution to the field of probabilistic modeling.

Implementation

A while back during covid I implemented a bunch of MCMC samplers for fun and uploaded them to pytorch_MCMC. Then the PyTorch teams implemented a series of functional API’s inspired by JAX’s functional approach.

Chief among them was the ability to evaluate multiple sets of parameters in parallel, which implicitly allowed to evaluate sets of intricate, nested parameters in parallel. That smelled like a nice application to run multiple MCMC chains over arbitrarily nested inputs in parallel.

I reimplemented the MCMC samplers in a functional way and uploaded them to a second branch of the original repository called pytorch_MCMC.